
【题目】如图,在△OAC中,以点O为圆心、OA长为半径作⊙O,作OB⊥OC交⊙O于点B,连接AB交OC于点D,∠CAD=∠CDA.

(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=10,OD=2,求线段AC的长.
【答案】(1)AC是⊙O的切线(2)线段AC的长为24
【解析】试题分析:(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,可得AC是⊙O的切线;
(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在Rt△OAC中,根据勾股定理来求AC的长度.
试题解析:解:(1)AC是⊙O的切线.证明:∵点A,B在⊙O上,∴OB=OA,∴∠OBA=∠OAB,∵∠CAD=∠CDA=∠BDO,∴∠CAD+∠OAB=∠BDO+∠OBA,∵BO⊥OC,
∴∠BDO+∠OBA=90°,∴∠CAD+∠OAB=90°,∴∠OAC=90°,即OA⊥AC,又∵OA是⊙O的半经,∴AC是⊙O的切线;
(2)设AC的长为x.∵∠CAD=∠CDA,∴CD的长为x.由(1)知OA⊥AC,
∴在Rt△OAC中,OA2+AC2=OC2,即102+x2=(2+x)2,∴x=24,
即线段AC的长为24.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
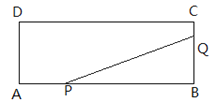
【题目】如图,矩形ABCD中,AB=16cm,AD=4cm,点P、Q分别从A、B同时出发,点P在边AB上沿AB方向以2cm/s的速度匀速运动,点Q在边BC上沿BC方向以1cm/s的速度匀速运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“我的中国梦”演讲比赛,有9名学生参加比赛,他们比赛的最终成绩各不相同,取前5名同学参加决赛.其中一名同学知道自己的分数后,要判断自己能否进入决赛,只需要知道这9名同学分数的( )
A. 中位数B. 众数C. 平均数D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5μm(0.0000025m)的颗粒物,含有大量有毒、有害物质,也称可入肺颗粒物.将0.0000025用科学记数法表示为( )
A.25×10﹣7
B.2.5×10﹣6
C.0.25×10﹣5
D.2.5×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com