
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
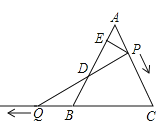
【答案】DE 的长不变,DE=3
【解析】试题分析:作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=![]() AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.
AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.
试题解析:过P 作PF∥QC

则△AFP是等边三角形,
∵P 、Q 同时出发、速度相同,即BQ=AP
∴BQ=PF
∴△DBQ≌△DFP,
知BD=DF而△APF 是等边三角形,PE ⊥AF,
∵AE=EF 又DE+(BD+AE)=AB=6,
∴DE+(DF+EF)=6 ,
即DE+DE=6,
∵DE=3 为定值,即DE 的长不变.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人练习短距离赛跑,测得甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑2秒,那么几秒钟后甲可以追上乙若设x秒后甲追上乙,列出的方程应为( )
A. 7x=6.5 B. 7x=6.5(x+2) C. 7(x+2)=6.5x D. 7(x﹣2)=6.5x
查看答案和解析>>
科目:初中数学 来源: 题型:
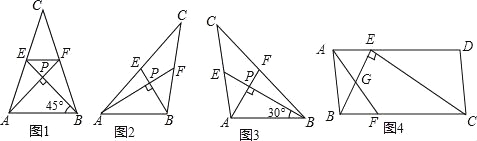
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线m上找出满足下列条件的点P.请保留作图痕迹,其中第(2)小题用尺规作图.
(1)点P到A、B距离之和最小时的位置;
(2)点P到A、B距离相等时的位置;
(3)点P到A、B的距离之差最大时P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,则点P的坐标为( )
A. (-5,2) B. (-5,-2) C. (-2,5) D. (-2,-5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com