
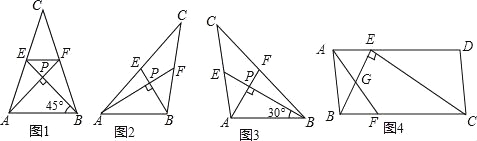
����Ŀ������˼����С����̽������ֱ�ߵ�λ�ù�ϵ��������ʱ�������ˡ��д������Ρ��������������ഹֱ�������γ�Ϊ���д������Ρ�����ͼ��1����ͼ��2����ͼ��3���У�AM��BN����ABC�����ߣ�AN��BN�ڵ�P������ABC�����������ξ�Ϊ���д������Ρ�����BC=a��AC=b��AB=c��
������̽����
��1����ͼ1����tan��PAB=1��c=4![]() ʱ��a= ��b= ��
ʱ��a= ��b= ��
��ͼ2������PAB=30�㣬c=2ʱ��a= ��b= ��
������֤����
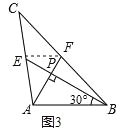
��2������۲죨1���еļ�����������a2��b2��c2����֮��Ĺ�ϵ���õ�ʽ��ʾ������������ͼ3֤����Ľ��ۣ�
����չ֤����
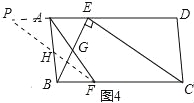
��3����ͼ4��ABCD�У�E��F�ֱ���AD��BC�����ȷֵ㣬��AD=3AE��BC=3BF������AF��BE��CE����BE��CE��E��AF��BE�ཻ��G��AD=3![]() ��AB=3����AF�ij���
��AB=3����AF�ij���
���𰸡���1��4![]() ��4
��4![]() ��
��![]() ��
��![]() ����2��a2+b2=5c2�����ɼ�����.(3)4.
����2��a2+b2=5c2�����ɼ�����.(3)4.
��������
�����������1��������֤����APB����PEF���ǵ���ֱ�������Σ����PA��PB��PE��PF�������ù��ɶ������ɽ�����⣮������EF����RT��PAB��RT��PEF�У�����30���������PA��PB��PE��PF�������ù��ɶ������ɽ�����⣮��2������a2+b2=5c2����MP=x��NP=y����AP=2x��BP=2y�����ù��ɶ����ֱ����a2��b2��c2���ɽ�����⣮��3��ȡAB�е�H������FH�����ӳ���DA���ӳ�����P�㣬����֤����ABF���д������Σ����ã�2���н����г����̼��ɽ�����⣮
�����������1���⣺��ͼ1�У���CE=AE��CF=BF��
��EF��AB��EF=![]() AB=2
AB=2![]() ��
��
��tan��PAB=1��
���PAB=��PBA=��PEF=��PFE=45�㣬
��PF=PE=2��PB=PA=4��
��AE=BF=![]() =2
=2![]() ��
��
��b=AC=2AE=4![]() ��a=BC=4
��a=BC=4![]() ��
��
��ͼ2�У�����EF��
����CE=AE��CF=BF��
��EF��AB��EF=![]() AB=1��
AB=1��
�ߡ�PAB=30�㣬
��PB=1��PA=![]() ��
��
��RT��EFP�У��ߡ�EFP=��PAB=30�㣬
��PE=![]() ��PF=
��PF=![]() ��
��
��AE=![]() =
=![]() ��BF=
��BF=![]() =
=![]() ��
��
��a=BC=2BF=![]() ��b=AC=2AE=
��b=AC=2AE=![]() ��
��
��2������
֤������ͼ3�У�����EF��
��AF��BE�����ߣ�
��EF��AB��EF=![]() AB��
AB��
���FPE�ס�APB��
��![]() =
=![]() =
=![]() ��
��
��FP=x��EP=y����AP=2x��BP=2y��
��a2=BC2=4BF2=4��FP2+BP2��=4x2+16y2��
b2=AC2=4AE2=4��PE2+AP2��=4y2+16x2��
c2=AB2=AP2+BP2=4x2+4y2��
��a2+b2=20x2+20y2=5��4x2+4y2��=5c2��
��3���⣺��ͼ4�У��ڡ�AGE�͡�FGB�У�
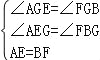 ��
��
���AGE�ա�FGB��
��BG=FG��ȡAB�е�H������FH�����ӳ���DA���ӳ�����P�㣬
ͬ����֤��APH�ա�BFH��
��AP=BF��PE=CF=2BF��
��PE��CF��PE=CF��
���ı���CEPF��ƽ���ı��Σ�
��FP��CE��
��BE��CE��
��FP��BE����FH��BG��
���ABF���д������Σ�
�ɣ�2����֪AB2+AF2=5BF2��
��AB=3��BF=![]() AD=
AD=![]() ��
��
��9+AF2=5����![]() ��2��
��2��
��AF=4��





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����³������ж�������˳���ǿ����Ķ�����������ɲ��ֵ����������غ����ֺ���ij������֯�����O�˲����ʽ𣬼ƻ�����ס������־�����Ʒ��2000��������������֪ÿ��������Ʒ�ļ۸��ÿ��������Ʒ�ļ۸��10Ԫ����350Ԫ���������Ʒ�ļ���ǡ������300Ԫ����������Ʒ�ļ�����ͬ
��1����ס������־�����Ʒÿ���ļ۸���Ƕ���Ԫ��
��2�������飬������������Ʒ�������������Ǽ�����Ʒ������3�������ð�����֯���մ�����ı���������2000����Ʒ����O�ʽ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ��l1��y����2x��2ƽ�ƺõ�ֱ��l2��y����2x��4��������ƽ�Ʒ�����ȷ����( )
A. ��l1����ƽ��3����λ���� B. ��l1����ƽ��6����λ����
C. ��l1����ƽ��2 ����λ���� D. ��l1����ƽ��4����λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A�á�B�á�C��1��2��3�����ABCһ����( )
A. ��������� B. �۽������� C. ֱ�������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��2m+1��ƽ��������5��3m+n+1��ƽ��������7����m+2n��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ�㣬���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D�����˶��������߶�ED�ij��Ƿ����仯��������䣬����߶�ED�ij�������仯��˵�����ɣ�
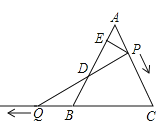
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x��x��2��=0�Ľ��ǣ� ��
A.x=0
B.x1=2
C.x1=0��x2=2
D.x=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ú����ú518�֣���ú����ú106�֣�Ϊ��ʹ��ú����ú����ú����2������Ҫ�Ӽ�ú����ú����ú������Ӽ�ú����úx�ֵ���ú��������з���Ϊ�� ��
A.518=2��106+x��
B.518��x=2��106
C.518��x=2��106+x��
D.518+x=2��106��x��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com