
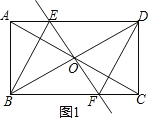
【题目】(1)如图1,在矩形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() ,且交
,且交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,且
,且![]() 平分
平分![]() .
.
①求证:四边形![]() 是菱形;
是菱形;
②直接写出![]() 的度数;
的度数;

(2)把(1)中菱形![]() 进行分离研究,如图2,
进行分离研究,如图2,![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() 为
为![]() 的中点,连接
的中点,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .试探究线段
.试探究线段![]() 与
与![]() 之间满足的关系,并说明理由;
之间满足的关系,并说明理由;
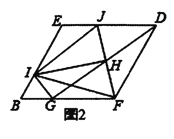
(3)把(1)中矩形![]() 进行特殊化探究,如图3,矩形
进行特殊化探究,如图3,矩形![]() 满足
满足![]() 时,点
时,点![]() 是对角线
是对角线![]() 上一点,连接
上一点,连接![]() ,作
,作![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .请直接写出线段
.请直接写出线段![]() 三者之间满足的数量关系.
三者之间满足的数量关系.

【答案】(1)①见解析;②60°;(2)见解析;(3)见解析.
【解析】
(1)①由△DOE≌△BOF,推出EO=OF,由OB=OD,推出四边形EBFD是平行四边形,再证明EB=ED即可;②先证明∠ABD=2∠ADB,推出∠ADB=30°,即可解决问题;
(2)延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,由菱形性质,
,由菱形性质,![]() ,得
,得![]() ,由此
,由此![]() ,由ASA可证得
,由ASA可证得![]() ,由此
,由此![]() ,故
,故
![]() ,由
,由![]() ,可证得
,可证得![]() 是等边三角形,可得
是等边三角形,可得![]() ,
,![]() ,由SAS可证
,由SAS可证![]() ,可得
,可得![]() ,即
,即![]() 是等边三角形,
是等边三角形,
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() ,由此可得
,由此可得![]() ;
;
(3)结论:EG2=AG2+CE2.如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,先证明△DEG≌△DEM,再证明△ECM是直角三角形即可解决问题.
(1)①证明:如图1中,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
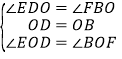 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形.
是菱形.
②∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() A=
A=![]() ,
,
∴![]() +
+![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴![]() ;
;
(2)结论:![]() .
.
理由:如图2中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
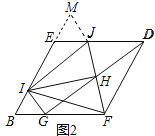
∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
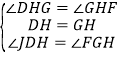 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
在![]() 和
和![]() 中,
中,
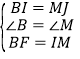 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)结论:![]() .
.
理由:如图3中,将△ADG绕点D逆时针旋转90°得到△DCM,
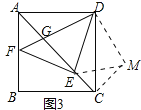
∵∠FAD+∠DEF=90°,
∴AFED四点共圆,
∴∠EDF=∠DAE=45°,∠ADC=90°,
∴∠ADF+∠EDC=45°,
∵∠ADF=∠CDM,
∴∠CDM+∠CDE=45°=∠EDG,
在△DEM和△DEG中,
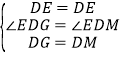 ,
,
∴△DEG≌△DEM,
∴GE=EM,
∵∠DCM=∠DAG=∠ACD=45°,AG=CM,
∴∠ECM=90°,
∴EC2+CM2=EM2,
∵EG=EM,AG=CM,
∴GE2=AG2+CE2.


科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(![]() ),王红家只有刻度不超过
),王红家只有刻度不超过![]() 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔![]() 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A. 没有加热时,油的温度是![]()
B. 加热![]() ,油的温度是
,油的温度是![]()
C. 估计这种食用油的沸点温度约是![]()
D. 每加热![]() ,油的温度升高
,油的温度升高![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
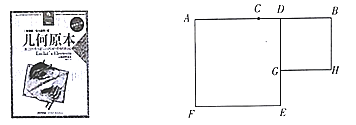
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
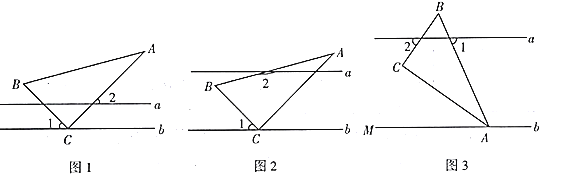
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
第1个式子: ![]()
第2个式子: ![]()
第3个式子: ![]()
第4个式子: ![]()
![]()
(1)可猜想第7个等式为 .
(2)探索规律,若字母![]() 表示自然数,请写出第
表示自然数,请写出第![]() 个等式 .
个等式 .
(3)试证明你写出的等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
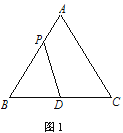
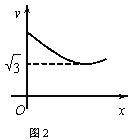
【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com