
ΓΨΧβΡΩΓΩ‘ΎΓΕΩΤ―ßΓΖΩΈ…œΘ§άœ ΠΫ≤ΒΫΈ¬Ε»ΦΤΒΡ Ι”ΟΖΫΖ®ΦΑ“ΚΧεΒΡΖ–Βψ ±Θ§ΚΟΤφΒΡΆθΚλΆ§―ßΉΦ±Η≤βΝΩ ≥”Ο”ΆΒΡΖ–ΒψΘ§“―÷Σ ≥”Ο”ΆΒΡΖ–ΒψΈ¬Ε»ΗΏ”ΎΥ°ΒΡΖ–ΒψΈ¬Ε»Θ®![]() Θ©Θ§ΆθΚλΦ“÷Μ”–ΩΧΕ»≤Μ≥§Ιΐ
Θ©Θ§ΆθΚλΦ“÷Μ”–ΩΧΕ»≤Μ≥§Ιΐ![]() ΒΡΈ¬Ε»ΦΤΘ§ΥΐΒΡΖΫΖ® «‘ΎΙχ÷–ΒΙ»κ“Μ–© ≥”Ο”ΆΘ§”ΟΟΚΤχ‘νΨυ‘»Φ”»»Θ§≤ΔΟΩΗτ
ΒΡΈ¬Ε»ΦΤΘ§ΥΐΒΡΖΫΖ® «‘ΎΙχ÷–ΒΙ»κ“Μ–© ≥”Ο”ΆΘ§”ΟΟΚΤχ‘νΨυ‘»Φ”»»Θ§≤ΔΟΩΗτ![]() ≤βΝΩ“Μ¥ΈΙχ÷–”ΆΈ¬Θ§≤βΝΩΒΟΒΫΒΡ ΐΨί»γœ¬±μΘΚ
≤βΝΩ“Μ¥ΈΙχ÷–”ΆΈ¬Θ§≤βΝΩΒΟΒΫΒΡ ΐΨί»γœ¬±μΘΚ
±Φδ | 0 | 10 | 20 | 30 | 40 |
”ΆΈ¬ | 10 | 30 | 50 | 70 | 90 |
ΆθΚλΖΔœ÷Θ§…’ΝΥ![]() ±Θ§”ΆΖ–ΧΎΝΥΘ§‘ρœ¬Ν–ΥΒΖ®≤Μ’ΐ»ΖΒΡ «Θ® Θ©
±Θ§”ΆΖ–ΧΎΝΥΘ§‘ρœ¬Ν–ΥΒΖ®≤Μ’ΐ»ΖΒΡ «Θ® Θ©
A. ΟΜ”–Φ”»» ±Θ§”ΆΒΡΈ¬Ε» «![]()
B. Φ”»»![]() Θ§”ΆΒΡΈ¬Ε» «
Θ§”ΆΒΡΈ¬Ε» «![]()
C. ΙάΦΤ’β÷÷ ≥”Ο”ΆΒΡΖ–ΒψΈ¬Ε»‘Φ «![]()
D. ΟΩΦ”»»![]() Θ§”ΆΒΡΈ¬Ε»…ΐΗΏ
Θ§”ΆΒΡΈ¬Ε»…ΐΗΏ![]()
ΓΨ¥πΑΗΓΩD
ΓΨΫβΈωΓΩ
ΗυΨί±μΗώ÷–ΒΡ ΐΨίΒΟΘΚΟΩΦ”»»10sΘ§Έ¬Ε»…ΐΗΏ20ΓφΘ§”…¥Υ÷π“ΜΫχ––Ζ÷ΈωΦ¥Ω…ΒΟ.
ΗυΨί±μΗώ÷–ΒΡ ΐΨίΒΟΘΚΟΜ”–Φ”»» ±Θ§Έ¬Ε»ΈΣ10ΓφΘ§ΟΩΦ”»»10sΘ§Έ¬Ε»…ΐΗΏ20ΓφΘ§
”…¥ΥΩ…ΒΟΦ”»»50s ±Θ§”ΆΒΡΈ¬Ε» «110ΓφΘ§
Ι ―ΓœνAΓΔBΒΡΥΒΖ®’ΐ»ΖΘ§≤ΜΖϊΚœΧβ“βΘ§
―ΓœνDΒΡΥΒΖ®≤Μ’ΐ»ΖΘ§ΖϊΚœΧβ“βΘ§
…’ΝΥ![]() ±Θ§”ΆΖ–ΧΎΝΥΘ§¥Υ ±”ΆΈ¬ΈΣ10+20ΓΝ110Γ¬10=230ΓφΘ§Ι C―Γœν’ΐ»ΖΘ§≤ΜΖϊΚœΧβ“βΘ§
±Θ§”ΆΖ–ΧΎΝΥΘ§¥Υ ±”ΆΈ¬ΈΣ10+20ΓΝ110Γ¬10=230ΓφΘ§Ι C―Γœν’ΐ»ΖΘ§≤ΜΖϊΚœΧβ“βΘ§
Ι ―ΓD.


 ”≈Β»…ζΧβΩβœΒΝ–¥πΑΗ
”≈Β»…ζΧβΩβœΒΝ–¥πΑΗ 53ΧλΧλΝΖœΒΝ–¥πΑΗ
53ΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
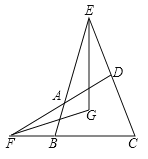
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎΥΡ±Ώ–ΈABCD÷–,E.FΖ÷±π «ΝΫΉιΕ‘±Ώ―”≥ΛœΏΒΡΫΜΒψ,EG.FGΖ÷±πΤΫΖ÷![]() .
.![]() ,»τ
,»τ![]() ,
,![]() ,‘ρ
,‘ρ![]() ΒΡ¥σ–Γ «_________________
ΒΡ¥σ–Γ «_________________
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘Ύ ΐ÷α…œΒψ![]() ±μ ΨΒΡ ΐΈΣ-2Θ§0Θ§6Θ°Βψ
±μ ΨΒΡ ΐΈΣ-2Θ§0Θ§6Θ°Βψ![]() ”κΒψ
”κΒψ![]() ÷°ΦδΒΡΨύάκ±μ ΨΈΣ
÷°ΦδΒΡΨύάκ±μ ΨΈΣ![]() Θ§Βψ
Θ§Βψ![]() ”κΒψ
”κΒψ![]() ÷°ΦδΒΡΨύάκ±μ ΨΈΣ
÷°ΦδΒΡΨύάκ±μ ΨΈΣ![]() Θ§Βψ
Θ§Βψ![]() ”κΒψ
”κΒψ![]() ÷°ΦδΒΡΨύάκ±μ ΨΈΣ
÷°ΦδΒΡΨύάκ±μ ΨΈΣ![]() Θ°
Θ°
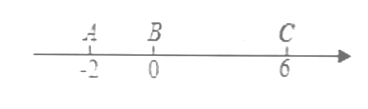
Θ®1Θ©«κ÷±Ϋ”–¥≥ωΫαΙϊΘ§![]() Θ°
Θ°![]() Θ°
Θ°![]() Θ°
Θ°
Θ®2Θ©Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣ
…œΒΡ“ΜΗωΕ·ΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣ![]() Θ§«κΜ·Φρ ΫΉ”Θ§
Θ§«κΜ·Φρ ΫΉ”Θ§![]() Θ®–¥≥ωΜ·ΦρΙΐ≥ΧΘ©
Θ®–¥≥ωΜ·ΦρΙΐ≥ΧΘ©
Θ®3Θ©Βψ![]() ΩΣ Φ‘Ύ ΐ÷α…œ‘ΥΕ·Θ§»τΒψ
ΩΣ Φ‘Ύ ΐ÷α…œ‘ΥΕ·Θ§»τΒψ![]() “‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΉσ‘ΥΕ·Θ§Ά§ ±Θ§Βψ
“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΉσ‘ΥΕ·Θ§Ά§ ±Θ§Βψ![]() ΚΆΒψ
ΚΆΒψ![]() Ζ÷±π“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΚΆ5ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ”“‘ΥΕ·Θ°«κΈ ΘΚ
Ζ÷±π“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΚΆ5ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ”“‘ΥΕ·Θ°«κΈ ΘΚ![]() ΒΡ÷Β «ΖώΥφΉ≈‘ΥΕ· ±Φδ
ΒΡ÷Β «ΖώΥφΉ≈‘ΥΕ· ±Φδ![]() ΒΡ±δΜ·Εχ±δΜ·ΘΩ»τ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ»τ≤Μ±δΘ§«κ«σΤδ÷Β
ΒΡ±δΜ·Εχ±δΜ·ΘΩ»τ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ»τ≤Μ±δΘ§«κ«σΤδ÷Β
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐ÷α…œ»ΐΒψ![]() Ε‘”ΠΒΡ ΐΖ÷±πΈΣ-1Θ§0Θ§3Θ§Βψ
Ε‘”ΠΒΡ ΐΖ÷±πΈΣ-1Θ§0Θ§3Θ§Βψ![]() ΈΣ ΐ÷α…œ»Έ“β“ΜΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣ
ΈΣ ΐ÷α…œ»Έ“β“ΜΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣ![]() Θ°
Θ°
Θ®1Θ©![]() ΒΡ≥ΛΈΣ_______ΘΜ
ΒΡ≥ΛΈΣ_______ΘΜ
Θ®2Θ©»γΙϊΒψ![]() ΒΫΒψ
ΒΫΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ΒΡΨύάκœύΒ»Θ§Ρ«Ο¥
ΒΡΨύάκœύΒ»Θ§Ρ«Ο¥![]() ΒΡ÷Β «_______ΘΜ
ΒΡ÷Β «_______ΘΜ
Θ®3Θ©»τΒψ![]() ΒΫΒψ
ΒΫΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ΒΡΨύάκ÷°ΚΆ «8Θ§Ρ«Ο¥
ΒΡΨύάκ÷°ΚΆ «8Θ§Ρ«Ο¥![]() ΒΡ÷Β «_______ΘΜ
ΒΡ÷Β «_______ΘΜ
Θ®4Θ©»γΙϊΒψ![]() “‘ΟΩΖ÷÷”1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»¥”Βψ
“‘ΟΩΖ÷÷”1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»¥”Βψ![]() œρΉσ‘ΥΕ·Θ§Ά§ ±Βψ
œρΉσ‘ΥΕ·Θ§Ά§ ±Βψ![]() ΚΆΒψ
ΚΆΒψ![]() Ζ÷±π“‘ΟΩΖ÷÷”2ΗωΒΞΈΜ≥ΛΕ»ΚΆΟΩΖ÷÷”3ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“≤œρΉσ‘ΥΕ·.…η
Ζ÷±π“‘ΟΩΖ÷÷”2ΗωΒΞΈΜ≥ΛΕ»ΚΆΟΩΖ÷÷”3ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“≤œρΉσ‘ΥΕ·.…η![]() Ζ÷÷” ±ΒψPΒΫΒψ
Ζ÷÷” ±ΒψPΒΫΒψ![]() ΓΔΒψ
ΓΔΒψ![]() ΒΡΨύάκœύΒ»Θ§Ρ«Ο¥
ΒΡΨύάκœύΒ»Θ§Ρ«Ο¥![]() ΒΡ÷Β «_______Θ°
ΒΡ÷Β «_______Θ°
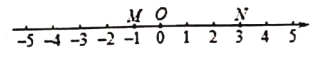
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–≈–Ε®÷–Θ§’ΐ»ΖΒΡΗω ΐ”–Θ® Θ©
ΔΌ“ΜΉιΕ‘±ΏΤΫ––Θ§“ΜΉιΕ‘±ΏœύΒ»ΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘΜ
ΔΎΕ‘Ϋ«œΏΜΞœύΤΫΖ÷«“œύΒ»ΒΡΥΡ±Ώ–Έ «ΨΊ–ΈΘΜ
ΔέΕ‘Ϋ«œΏΜΞœύ¥Ι÷±ΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΜ
ΔήΕ‘Ϋ«œΏΜΞœύ¥Ι÷±ΤΫΖ÷«“œύΒ»ΒΡΥΡ±Ώ–Έ «’ΐΖΫ–ΈΘ§
A. 1ΗωB. 2ΗωC. 3ΗωD. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΤΫΗΏΦ·Ά≈”–œόΙΪΥΨΉΦ±Η…ζ≤ζΦΉΓΔ““ΝΫ÷÷ΩΣΙΊΘ§Ι≤8ΆρΦΰΘ§œζΆυΕΪΡœ―«ΙζΦ“ΚΆΒΊ«χΓΘ“―÷Σ2ΦΰΦΉ÷÷ΩΣΙΊ”κ3Φΰ““÷÷ΩΣΙΊœζ έΕνœύΆ§ΘΜ3ΦΰΦΉ÷÷ΩΣΙΊ±»2Φΰ““÷÷ΩΣΙΊΒΡœζ έΕνΕύ1500‘ΣΓΘ
(1)ΦΉ÷÷ΩΣΙΊ”κ““÷÷ΩΣΙΊΒΡœζ έΒΞΦέΗςΈΣΕύ…Ό‘Σ?
(2)»τΦΉΓΔ““ΝΫ÷÷ΩΣΙΊΒΡœζ έΉή ’»κ≤ΜΒΆ”Ύ5400Άρ‘ΣΘ§‘ρ÷Ν…Όœζ έΦΉ÷÷ΩΣΙΊΕύ…ΌΆρΦΰΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦ1Θ§‘ΎΨΊ–Έ![]() ÷–Θ§Ε‘Ϋ«œΏ
÷–Θ§Ε‘Ϋ«œΏ![]() ”κ
”κ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής÷±œΏ
Ής÷±œΏ![]() Θ§«“ΫΜ
Θ§«“ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§«“
Θ§«“![]() ΤΫΖ÷
ΤΫΖ÷![]() .
.
ΔΌ«σ÷ΛΘΚΥΡ±Ώ–Έ![]() «Νβ–ΈΘΜ
«Νβ–ΈΘΜ
ΔΎ÷±Ϋ”–¥≥ω![]() ΒΡΕ» ΐΘΜ
ΒΡΕ» ΐΘΜ

Θ®2Θ©Α―Θ®1Θ©÷–Νβ–Έ![]() Ϋχ––Ζ÷άκ―–ΨΩΘ§»γΆΦ2Θ§
Ϋχ––Ζ÷άκ―–ΨΩΘ§»γΆΦ2Θ§![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() ±Ώ…œΘ§«“
±Ώ…œΘ§«“![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§Ν§Ϋ”
ΒΡ÷–ΒψΘ§Ν§Ϋ”![]() Θ§≤Δ―”≥Λ
Θ§≤Δ―”≥Λ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() . ‘ΧΫΨΩœΏΕΈ
. ‘ΧΫΨΩœΏΕΈ![]() ”κ
”κ![]() ÷°Φδ¬ζΉψΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
÷°Φδ¬ζΉψΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
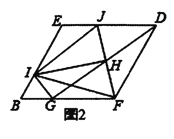
Θ®3Θ©Α―Θ®1Θ©÷–ΨΊ–Έ![]() Ϋχ––ΧΊ βΜ·ΧΫΨΩΘ§»γΆΦ3Θ§ΨΊ–Έ
Ϋχ––ΧΊ βΜ·ΧΫΨΩΘ§»γΆΦ3Θ§ΨΊ–Έ![]() ¬ζΉψ
¬ζΉψ![]() ±Θ§Βψ
±Θ§Βψ![]() «Ε‘Ϋ«œΏ
«Ε‘Ϋ«œΏ![]() …œ“ΜΒψΘ§Ν§Ϋ”
…œ“ΜΒψΘ§Ν§Ϋ”![]() Θ§Ής
Θ§Ής![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() .«κ÷±Ϋ”–¥≥ωœΏΕΈ
.«κ÷±Ϋ”–¥≥ωœΏΕΈ![]() »ΐ’Ώ÷°Φδ¬ζΉψΒΡ ΐΝΩΙΊœΒ.
»ΐ’Ώ÷°Φδ¬ζΉψΒΡ ΐΝΩΙΊœΒ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
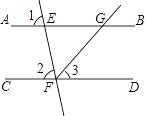
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏABΓΔCD±Μ÷±œΏEFΥυΫΊΘ§FGΤΫΖ÷ΓœEFDΘ§Γœ1=Γœ2=80ΓψΘ§«σΓœBGFΒΡΕ» ΐΘ°
ΫβΘΚ“ρΈΣΓœ1=Γœ2=80ΓψΘ®“―÷ΣΘ©Θ§
Υυ“‘ABΓΈCD__________
Υυ“‘ΓœBGF+Γœ3=180Γψ__________
“ρΈΣΓœ2+ΓœEFD=180ΓψΘ®ΝΎ≤ΙΫ«ΒΡ–‘÷ Θ©Θ°
Υυ“‘ΓœEFD=________Θ°Θ®Β» Ϋ–‘÷ Θ©Θ°
“ρΈΣFGΤΫΖ÷ΓœEFDΘ®“―÷ΣΘ©Θ°
Υυ“‘Γœ3=________ΓœEFDΘ®Ϋ«ΤΫΖ÷œΏΒΡ–‘÷ Θ©Θ°
Υυ“‘Γœ3=________Θ°Θ®Β» Ϋ–‘÷ Θ©Θ°
Υυ“‘ΓœBGF=________Θ°Θ®Β» Ϋ–‘÷ Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©Ϋβ≤ΜΒ» ΫΘΚx+4ΘΨ3Θ®x©¹2Θ©≤ΔΑ―ΫβΦ·‘Ύ ΐ÷α…œ±μ Ψ≥ωά¥Θ°
![]()
Θ®2Θ©x»ΓΡΡ–©’ϊ ΐ ±Θ§≤ΜΒ» Ϋ5x©¹1ΘΦ3Θ®x+1Θ©”κ![]() ©¹1Γί©¹2ΕΦ≥…ΝΔΘ°
©¹1Γί©¹2ΕΦ≥…ΝΔΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com