
【题目】(1)如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边,在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?若成立,请证明;
(3)Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;
Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

【答案】(1)AF=BD,理由见解析;(2)AF与BD在(1)中的结论成立,理由见解析;(3)Ⅰ. AF+BF′=AB,理由见解析,Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′,理由见解析.
【解析】
(1)由等边三角形的性质得BC=AC,∠BCA=60°,DC=CF,∠DCF=60°,从而得∠BCD=∠ACF,根据SAS证明△BCD≌△ACF,进而即可得到结论;
(2)根据SAS证明△BCD≌△ACF,进而即可得到结论;
(3)Ⅰ.易证△BCD≌△ACF(SAS),△BCF′≌△ACD(SAS),进而即可得到结论;Ⅱ.证明△BCF′≌△ACD,结合AF=BD,即可得到结论.
(1)结论:AF=BD,理由如下:
如图1中,∵△ABC是等边三角形,
∴BC=AC,∠BCA=60°,
同理知,DC=CF,∠DCF=60°,
∴∠BCA-∠DCA=∠DCF-∠DCA,即:∠BCD=∠ACF,
在△BCD和△ACF中,
∵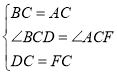 ,
,
∴△BCD≌△ACF(SAS),
∴BD=AF;
(2)AF与BD在(1)中的结论成立,理由如下:
如图2中,∵△ABC是等边三角形,
∴BC=AC,∠BCA=60°,
同理知,DC=CF,∠DCF=60°,
∴∠BCA+∠DCA=∠DCF+∠DCA,即∠BCD=∠ACF,
在△BCD和△ACF中,
∵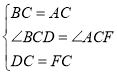 ,
,
∴△BCD≌△ACF(SAS),
∴BD=AF;
(3)Ⅰ.AF+BF′=AB,理由如下:
由(1)知,△BCD≌△ACF(SAS),则BD=AF;
同理:△BCF′≌△ACD(SAS),则BF′=AD,
∴AF+BF′=BD+AD=AB;
Ⅱ.Ⅰ中的结论不成立,新的结论是AF=AB+BF′,理由如下:
同理可得:![]() ,
,![]() ,
,
在△BCF′和△ACD中,
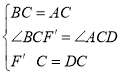 ,
,
∴△BCF′≌△ACD(SAS),
∴BF′=AD,
又由(2)知,AF=BD,
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.


科目:初中数学 来源: 题型:
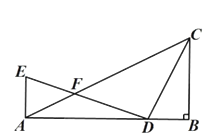
【题目】如图,在△ABC中,∠ABC=90°,D为AB边上一点(BD<BC),AE⊥AB,AE=BD,连接DE交AC于F,若∠AFE=45°,AD=3![]() ,CD=5,则线段AC的长度为_________.
,CD=5,则线段AC的长度为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )

A. ① B. ② C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD·OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2, ![]() .
.
①求⊙O的半径;②求sin∠BAD的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)若AC=6,BC=8,OA=2,求线段AD和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() A运动,到
A运动,到![]() 点停止,若点
点停止,若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() ,如图2是点
,如图2是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,图3是点
的函数关系图象,图3是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,根据图象:
的函数关系图象,根据图象:
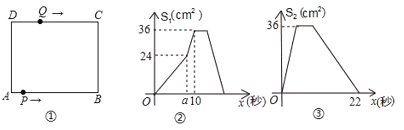
(1)点![]() 经过______秒运动到
经过______秒运动到![]() 点,此时
点,此时![]() 的面积为______;点
的面积为______;点![]() 经过______秒运动到
经过______秒运动到![]() 点;
点;
(2)![]() ______秒,
______秒,![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(3)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,点
,点![]() 到点
到点![]() 还需要走的路程为
还需要走的路程为![]() ,请分别写出改变速度后
,请分别写出改变速度后![]() 、
、![]() 与出发后的运动时间
与出发后的运动时间![]() (秒)的函数关系式;
(秒)的函数关系式;
(4)直接写出![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(2,-4)在正比例函数y=kx的图象上。
(1)求k的值;
(2)若点(-1,m)在函数y=kx的图象上,试求出m的值;
(3)若A(![]() ,y1),B(-2,y2),C(1,y3)都在此函数图象上,试比较y1,y2,y3的大小。
,y1),B(-2,y2),C(1,y3)都在此函数图象上,试比较y1,y2,y3的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com