
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() A运动,到
A运动,到![]() 点停止,若点
点停止,若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() ,如图2是点
,如图2是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,图3是点
的函数关系图象,图3是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() 的函数关系图象,根据图象:
的函数关系图象,根据图象:
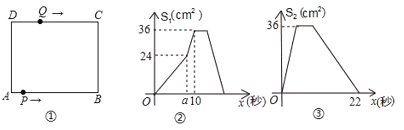
(1)点![]() 经过______秒运动到
经过______秒运动到![]() 点,此时
点,此时![]() 的面积为______;点
的面积为______;点![]() 经过______秒运动到
经过______秒运动到![]() 点;
点;
(2)![]() ______秒,
______秒,![]() ______
______![]() ,
,![]() ______
______![]() ;
;
(3)设点![]() 离开点
离开点![]() 的路程为
的路程为![]() ,点
,点![]() 到点
到点![]() 还需要走的路程为
还需要走的路程为![]() ,请分别写出改变速度后
,请分别写出改变速度后![]() 、
、![]() 与出发后的运动时间
与出发后的运动时间![]() (秒)的函数关系式;
(秒)的函数关系式;
(4)直接写出![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
【答案】(1)10;36;6;(2)8;2;1;(3)y1=2x-8(x>8);y2==22-x(x>8);(4)10
【解析】
(1)先求得点P到达B点时△APD的面积,然后结合图2中的图像分析求得时间,然后求出点Q到达点C时△AQD的面积,然后结合Q的运动速度分析求得时间;
(2)根据题意和S△APD求出a,b,c的值;
(3)首先求出y1,y2关于x的等量关系;
(4)根据题意可得y1=y2求出x的值;
解:(1)由题意可知![]() ,
,![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,
∴在矩形ABCD中,AD=BC=6
∴点![]() 运动到
运动到![]() 点时,
点时,![]()
∴由图2可知,当![]() 时,x=10,即点P运动到点B需要10秒
时,x=10,即点P运动到点B需要10秒
又由图2可知,当![]() 时,
时,![]()
∴此时AP=8,即8秒时P,Q同时改变速度
同理,当点Q运动到点C时,![]()
∴点Q到达点C的时间为![]()
故答案为:10;36;6;
(2)观察图象得,S△APQ=![]() PAAD=
PAAD=![]() ×(1×a)×6=24,
×(1×a)×6=24,
解得a=8(秒)
b=![]() =2(厘米/秒)
=2(厘米/秒)
(22-8)c=(12×2+6)-2×8
解得c=1(厘米/秒)
故答案为:8;2;1
(3)依题意得:y1=1×8+2(x-8),
即:y1=2x-8(
y2=(30-2×8)-1×(x-8)
=22-x(x>8)
(4)据题意,当y1=y2,P与Q相遇,
即2x-8=(22-x),
解得x=10.
故出发10s时P、Q相遇.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店原来将进货价为8元的商品按10元售出,每天可销售200件.现在采用提高售价,减少进货量的方法来增加利润,已知每件商品涨价1元,每天的销售量就减少20件.设这种商品每个涨价![]() 元.
元.
(1)填空:原来每件商品的利润是 元,涨价后每件商品的实际利润是 元 (可用含![]() 的代数式表示);
的代数式表示);
(2)为了使每天获得700元的利润,售价应定为多少元?
(3)售价定为多少元时,每天利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边,在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?若成立,请证明;
(3)Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;
Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
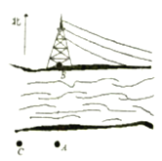
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



查看答案和解析>>
科目:初中数学 来源: 题型:
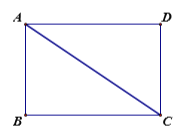
【题目】已知,如图:一张矩形纸片![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上一动点,将矩形沿
边上一动点,将矩形沿![]() 折叠,要使点
折叠,要使点![]() 落在
落在![]() 上,则折痕
上,则折痕![]() 的长度是________;若点
的长度是________;若点![]() 落在
落在![]() 上,则折痕
上,则折痕![]() 与
与![]() 的位置关系是__________.若翻折后
的位置关系是__________.若翻折后![]() 点的对应点是
点的对应点是![]() 点,连接
点,连接![]() ,则在点
,则在点![]() 运动的过程中,
运动的过程中,![]() 的最小值是______.
的最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com