
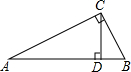
 如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,求sinA,sin∠ACD.
如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,求sinA,sin∠ACD. 分析 根据在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,可得CD的长,∠A=∠BCD,∠ACD=∠B,从而可以求得sinA,sin∠ACD的值.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}=\sqrt{{8}^{2}-{5}^{2}}=\sqrt{39}$.
∴sinB=$\frac{CD}{BC}=\frac{\sqrt{39}}{8}$,sin∠BCD=$\frac{BD}{BC}=\frac{5}{8}$.
∵∠ACB=90°,CD为斜边AB上的高,
∴∠BDC=90°.
∴∠B+∠BCD=90°,∠B+∠A=90°,∠ACD+∠BCD=90°.
∴∠A=∠BCD,∠ACD=∠B.
∴sinA=sin∠BCD=$\frac{BD}{BC}=\frac{5}{8}$,sin∠ACD=sinB=$\frac{CD}{BC}=\frac{\sqrt{39}}{8}$.
即sinA=$\frac{5}{8}$,sin∠ACD=$\frac{\sqrt{39}}{8}$.
点评 本题考查解直角三角形,解题的关键是利用数学中转化的思想,进行角的转化,从而可以求得所求角的函数值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 每个内角都是120°的六边形一定是正六边形 | |
| B. | 正n边形的对称轴不一定有n条 | |
| C. | 正n边形的每一个外角度数等于它的中心角度数 | |
| D. | 正多边形一定既是轴对称图形,又是中心对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com