
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
分析 (1)根据平均数的定义进而求出;利用方差的公式分别求得甲、乙两人的方差;
(2)利用标准差的意义进而分析得出即可;
(3)利用达到98分以上才可能进入决赛,结合两人超过98分的次数即可得出答案.
解答 解:(1)$\overline{x}$甲=$\frac{1}{11}$(98+100+100+90+96+91+89+99+100+100+93)=96(分),
$\overline{x}$乙=$\frac{1}{11}$(98+99+96+94+95+92+92+98+96+99+97)=96(分);
${S}_{甲}^{2}$=$\frac{1}{11}$[(98-96)2+(100-96)2+(100-96)2+(90-96)2+(96-96)2+(91-96)2+(89-96)2+(99-96)2+(100-96)2+(100-96)2+(93-96)2]
=$\frac{1}{11}$(4+16+16+36+0+25+49+9+16+16+9)
=$\frac{196}{11}$;
${S}_{乙}^{2}$=$\frac{1}{11}$[(98-96)2+(99-96)2+(96-96)2+(94-96)2+(95-96)2+(92-96)2+(92-96)2+(98-96)2+(96-96)2+(99-96)2+(97-96)2]
=$\frac{1}{11}$(4+9+0+4+1+16+16+4+0+9+1)
=$\frac{64}{11}$;
(2)由以上所求得出:两人平均成绩相同,甲的标准差大于乙的标准差,故甲的成绩不稳定;
(3)∵历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,甲的成绩有6次超过98分,乙的成绩有4次超过98分,
∴应选甲谁参加这项竞赛.
点评 此题主要考查了方差以及加权平均数,一般地设n个数据,x1,x2,…xn,平均数$\overline{x}$=$\frac{1}{n}$(x1+x2+x3…+xn),方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]它反映了一组数据的波动大小,方差越大,波动性越大,方差越小,波动性越小.学会分析数据和统计量,从而得出正确的结论.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
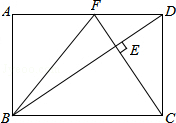 在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF,若点F为AD的中点,则$\frac{AB}{BC}$=( )
在矩形ABCD中,CF⊥BD分别交BD、AD于点E、F,连接BF,若点F为AD的中点,则$\frac{AB}{BC}$=( )| A. | 1:$\sqrt{3}$ | B. | 2:$\sqrt{3}$ | C. | 1:$\sqrt{2}$ | D. | $\sqrt{2}$:$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x-8=4x-2 | B. | 5x+8=10x+7 | C. | 13x-5=7x+13 | D. | 12x-4=5x+7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com