
分析 先求出已知算式的结果,根据求出的结果得出规律,根据规律得出答案即可.
解答 解:∵$\sqrt{{9}^{2}+19}$
=$\sqrt{{9}^{2}+9+10}$
=$\sqrt{9×(9+1)+10}$
=$\sqrt{9×10+10}$
=$\sqrt{10×(9+1)}$
=$\sqrt{10×10}$
=10,
同理$\sqrt{{99}^{2}+199}$=100,
$\sqrt{{999}^{2}+1999}$=1000,
$\sqrt{{9999}^{2}+19999}$=10000,
∴$\sqrt{\underset{\underbrace{99…{9}^{2}}}{2015个9}+\underset{\underbrace{199…9}}{2015个9}}$
=100…0(共2015个0)
=102015,
故答案为:102015.
点评 本题考查了二次根式的性质的应用,能根据已知算式得出规律是解此题的关键,题目是一道比较好的题目,有一点的难度.


科目:初中数学 来源: 题型:填空题
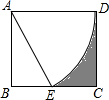 如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)
如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
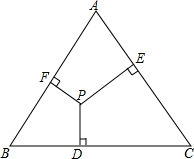 有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50 | 51~100 | 100人以上 |
| 每人门票 | 20元 | 18元 | 15元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com