
| 购票人数 | 1~50 | 51~100 | 100人以上 |
| 每人门票 | 20元 | 18元 | 15元 |
分析 (1)甲团人数少于50人,乙团人数不超过100人,15×100=1500<1545,所以乙团的人数不少于50人,不超过100人.
(2)利用本题中的相等关系:“两团共计应付门票费1950元”和“总计应付门票费1545元”,列方程组求解即可;
(3)按照实有人数购票和购买51张票两种方法计算比较得出答案即可.
解答 解:(1)假设乙团的人数少于50,则甲、乙两旅行团人数少于100.
∵1545÷15=103,
1950÷18=108$\frac{1}{3}$,
1950÷20=97.5
1950不是18的倍数,
∴乙团的人数不少于50人,不超过100人,且总人数会超过100;
(2)设甲、乙两旅行团分别有x人、y人.
$\left\{\begin{array}{l}{20x+18y=1950}\\{15(x+y)=1545}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{x=48}\\{y=55}\end{array}\right.$.
答:甲、乙两旅行团分别有48人、55人.
(3)甲旅行团购买51张票省钱.
理由:
单独购票:48×20=960元,
购买51张票:51×18=918元,
960>918,
所以购买51张票更省钱.
点评 此题考查二元一次方程组的实际运用,根据数据的特点,找出问题蕴含的数量关系是解决问题的关键.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
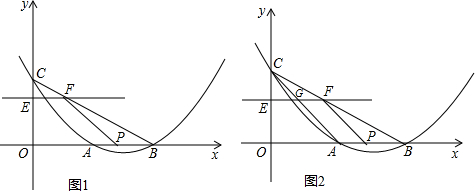
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com