
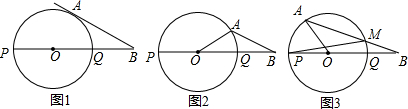
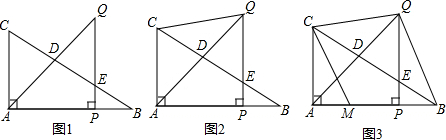
分析 (1)连接OA,根据直角三角形的性质求出∠B的度数,得到∠AOB的度数,根据弧长的计算公式求出点A走过的路径;
(2)根据直线与圆相切时,∠AOB的度数确定α的范围;
(3)连接MQ,根据三角形的中位线定理证明BM=MA,根据切割线定理求出AB的长.
解答 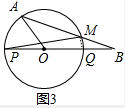
 解:(1)如图1,连接OA,
解:(1)如图1,连接OA,
∵直线AB与圆O相切,∴∠OAB=90°,又OA=$\frac{1}{2}$OB,
∴∠B=30°,则∠AOB=60°,
∴点A走过的路径为:$\frac{60π×1}{180}$=$\frac{π}{3}$;
(2)由(1)可知,当∠AOB=60°时,直线AB与圆O相切,
∴0°≤α≤60°;
(3)如图3,连接MQ,
∵PQ为圆O的直径,∴∠PMQ=90°,又AO⊥PM,
∴AO∥MQ,又BQ=OQ,
∴BM=MA,
由切割线定理,BM•BA=BQ•BP,
$\frac{1}{2}$AB2=1×3,
AB=$\sqrt{6}$.
点评 本题考查的是直线与圆相切、弧长的计算和切割线定理的应用,掌握弧长的计算公式和切割线定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 线段EF | B. | 线段DE | C. | 线段CE | D. | 线段BE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
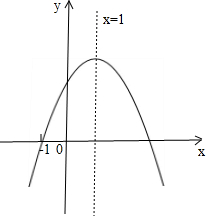
| A. | a>0 | B. | -1是方程ax2+bx+c=0的一个根 | ||
| C. | a+b+c=0 | D. | 当x<1时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
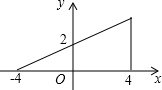 如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )
如图,若点P为函数y=kx+b(-4≤x≤4)图象上的一动点,m表示点P到原点O的距离,则下列图象中,能表示m与点P的横坐标x的函数关系的图象大致是( )| A. | 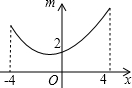 | B. | 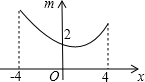 | C. | 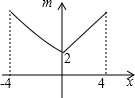 | D. | 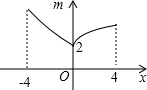 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com