
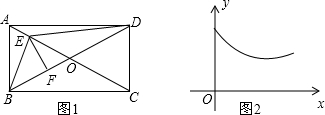
| A. | 线段EF | B. | 线段DE | C. | 线段CE | D. | 线段BE |
分析 作BN⊥AC,垂足为N,FM⊥AC,垂足为M,DG⊥AC,垂足为G,分别找出线段EF、CE、BE最小值出现的时刻即可得出结论.
解答 解:作BN⊥AC,垂足为N,FM⊥AC,垂足为M,DG⊥AC,垂足为G.
由题意:当点E与点O重合时,即AE=$\frac{1}{2}AC$时,FE有最小值0,与函数图象不符,故A错误;
由垂线段最短可知:当点E与点G重合时,即AE>$\frac{1}{2}AC$时,DE有最小值,故B正确;
∵CE=AC-AE,CE随着AE的增大而减小,故C错误;
由垂线段最短可知:当点E与点N重合时,即AE<$\frac{1}{2}AC$时,BE有最小值,与函数图象不符,故D错误;
故选:B.
点评 本题主要考查的是动点问题的函数图象,根据垂线段最短确定出函数最小值出现的时刻是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:底与腰的比是$\frac{\sqrt{5}-1}{2}$的等腰三角形叫做黄金等腰三角形.
定义:底与腰的比是$\frac{\sqrt{5}-1}{2}$的等腰三角形叫做黄金等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
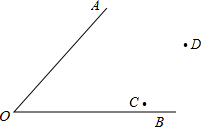 OA、OB为两条笔直的公路,C、D为两个工厂,现欲在附近建一个货运站,使得它到两条公路距离相等,到两家工厂距离也相等.请作出符合条件的货运站P.不写作法,保留作图痕迹.
OA、OB为两条笔直的公路,C、D为两个工厂,现欲在附近建一个货运站,使得它到两条公路距离相等,到两家工厂距离也相等.请作出符合条件的货运站P.不写作法,保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
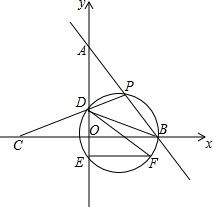 如图,在平面直角坐标系中,O为坐标原点,直线y=-$\frac{4}{3}$x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.
如图,在平面直角坐标系中,O为坐标原点,直线y=-$\frac{4}{3}$x+4与x轴交于点B,与y轴交于点A,点C在x轴的负半轴上,并且OC=OB,一动点P在射线AB上运动,连结CP交y轴于点D,连结BD.过B,P,D三点作圆,交y轴与点E,过点E作EF∥x轴,交圆于点F,连结BF,DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com