
分析 该题需要分类讨论:相遇前相距90km和相遇后相距90km两种情况.根据路程=时间×速度列出方程并解答.
解答 解:设慢车的速度为akm/h,则快车的速度为:1.5akm/h,
则360÷3=a+1.5a,
解得:a=48,
则快车的速度为:1.5×48=72(km/h)
①未相遇时,设它们出发x小时后相距90km.
则根据题意,得
48x+72x=360-90.
解得 x=2.25.
②相遇后,设它们出发y小时后相距90km.则
48y+72y=360+90.
解这个方程得:y=3.75.
答:两车出发后2.25小时或3.75小时相距90km.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
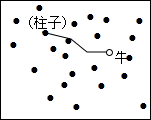 在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示.
在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
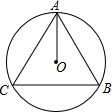 如图,△ABC的三个顶点都在圆O上,AO是∠BAC的角平分线,下列说法一定成立的是( )
如图,△ABC的三个顶点都在圆O上,AO是∠BAC的角平分线,下列说法一定成立的是( )| A. | △ABC是等腰三角形,且AC=BC | B. | △ABC是等腰三角形,且AC=AB | ||
| C. | △ABC是等腰三角形,且AB=BC | D. | △ABC是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
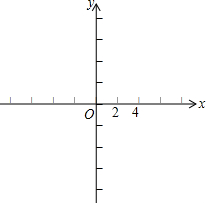 如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个数不是正数就是负数 | |
| B. | 正数和分数统称为有理数 | |
| C. | 正数和负数统称为有理数 | |
| D. | 有理数中有最小的正整数,最大的负整数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com