Question

如图，抛物线y=﹣x2+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．

（1）求tan∠DBC的值；

（2）点P为抛物线上一点，且∠DBP=45°，求点P的坐标．

 

 

Answer 1

（1）tan∠DBC=；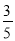

（2）P（﹣，）．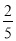

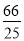【解析】

试题分析：（1）连接CD，过点D作DE⊥BC于点E．利用抛物线解析式可以求得点A、B、C、D的坐标，则可得CD//AB，OB=OC，所以∠BCO=∠BCD=∠ABC=45°．由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4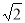，BE=BC﹣DE=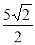．由此可知tan∠DBC=；

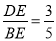（2）过点P作PF⊥x轴于点F．由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC，利用（1）中的结果得到：tan∠PBF=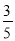．设P（x，﹣x2+3x+4），则利用锐角三角函数定义推知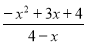=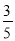，通过解方程求得点P的坐标为（﹣，）．

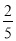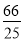试题解析：

（1）令y=0，则﹣x2+3x+4=﹣（x+1）（x﹣4）=0，

解得 x1=﹣1，x2=4．

∴A（﹣1，0），B（4，0）．

当x=3时，y=﹣32+3×3+4=4，

∴D（3，4）．

如图，连接CD，过点D作DE⊥BC于点E．

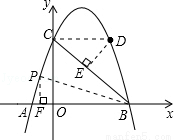
∵C（0，4），

∴CD//AB，

∴∠BCD=∠ABC=45°．

在直角△OBC中，∵OC=OB=4，

∴BC=4．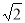

在直角△CDE中，CD=3．

∴CE=ED=，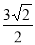

∴BE=BC﹣DE=．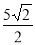

∴tan∠DBC=；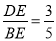

（2）过点P作PF⊥x轴于点F．

∵∠CBF=∠DBP=45°，

∴∠PBF=∠DBC，

∴tan∠PBF=．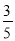

设P（x，﹣x2+3x+4），则=，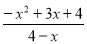

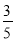解得 x1=﹣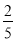，x2=4（舍去），

∴P（﹣，）．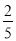

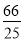考点：1、二次函数；2、勾股定理；3、三角函数