
ijУΪ���˽ⱾУ���꼶ѧ����������������������Ϊ�������ӣ���Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ�������Ծ��꼶�IJ���ѧ�������˳������飬�������������������������²�������ͳ��ͼ�����в��������ضȽ��������ĺ����жȽ���������2����

�������������Ϣ����������⣺
��1���ε����ѧ��������
��2����ȫ����ͳ��ͼ��������ͳ��ͼ�У��������ӡ���Ӧ���ε�Բ�ĽǶ�������144���ȣ�
��3������У���꼶ѧ����1050�ˣ�������Ƹ�У���꼶���ӣ�������Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ���ѧ����Լ�ж����ˣ�
��������
�����������1��������Ƚ��ӵ�������14�ˣ�ռ��������28%�����������������
��2�����жȽ��ӵ�������x�ˣ��������ضȽ��������ĺ�2x���з������x��ֵ��������ò����ӵ�������Ȼ������360����Զ�Ӧ�İٷֱȼ������Բ�ĽǵĶ�����
��3���������������Զ�Ӧ�İٷֱȼ�����⣮
�����������1�����ε����ѧ�����ǣ�14��28%=50���ˣ���
��2�����жȽ��ӵ�������x�ˣ��������ضȽ��������ĺ�2x����x+2x+14=50��
��ã�x=12��
���жȽ��ӵ�������12�������ӵ������ǣ�24��4=20���ˣ���
�����ӡ���Ӧ���ε�Բ�ĽǶ����ǣ�360���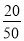 =144�㣻
=144�㣻
��3��1050��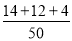 =630���ˣ���
=630���ˣ���
�𣺸�У���꼶���ӣ�������Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ���ѧ����Լ630�ˣ�
���㣺1������ͳ��ͼ2������ͳ��ͼ��3����������������.


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ�걱����˳�����п�һģ��ѧ�Ծ��������棩 ���ͣ������
��֪С�ϵ�����Ϊ1.8������̫�����µĵ���Ӱ��Ϊ2.4��������ʱ���һ�����ͬһ�����Ӱ��Ϊ20��������˸�ӦΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������绯������ѧ�������棩 ���ͣ������
��ͼ��������y=��x2+3x+4��x�ύ��A��B���㣬��y�ύ��C�㣬��D�����������Һ�����Ϊ3��
��1����tan��DBC��ֵ��
��2����PΪ��������һ�㣬����DBP=45�㣬���P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������绯������ѧ�������棩 ���ͣ������
һ�����ε�Բ�Ľ�Ϊ120�㣬�뾶Ϊ3����������ε����Ϊ��������������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ��������绯������ѧ�������棩 ���ͣ������
��2014���෴���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ĵ����������ѧ�������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���A��0��4����B��3��0��������AB������AOB�ع���B��ֱ���۵���ʹ��A����x���ϵĵ�A�䴦���ۺ����ڵ�ֱ�߽�y���������ڵ�C����ֱ��BC�Ľ���ʽΪ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������ĵ����������ѧ�������棩 ���ͣ������
ij����Ʒÿ���ı��Ϊ240Ԫ������۵İ�������ʱ��ÿ�����ܻ���20%����������Ʒÿ���Ľ���Ϊ�� ��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ����������������ѧ�������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=ax+b��ͼ����x���ཻ�ڵ�A��-2��0������y�ύ�ڵ�C���뷴�������� �ڵ�һ�����ڵ�ͼ���ڵ�B��m��n��������OB����S��AOB=6��S��BOC=2��
�ڵ�һ�����ڵ�ͼ���ڵ�B��m��n��������OB����S��AOB=6��S��BOC=2��
��1����һ�κ����ı���ʽ��
��2�����������ı���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014����б�ҵ��ѧ���ԣ�������������������ѧ�������棩 ���ͣ�ѡ����
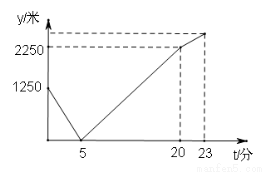
�糿��С������ͨ��ѧУΨһ��һ��·��ֱ·����ѧ��;�з����������У�ͣ���������绰������ӵ��绰����Ϸ������ϸ���ѧУ��ͬʱС�շ��أ�����������С����������ѧУ������ؼң�15�������赽�ң��پ���3����С�յ���ѧУ��С��ʼ����100��/�ֵ��ٶȲ��У�С�պ�����ľ���y����λ���ף���С�մ���绰��IJ���ʱ��t����λ���֣�֮��ĺ�����ϵ��ͼ����������˵����
����绰ʱ��С�պ�����ľ���Ϊ1250�ף�
������绰����23����С�յ���ѧУ��
��С�պ���������������ؼҵ��ٶ�Ϊ150��/�֣�
��С�ռ���ѧУ�ľ���Ϊ2550�ף�������ȷ�ĸ����ǣ�������
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com