
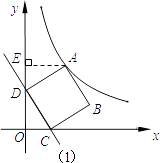
【题目】如图,在平面直角坐标系中,一次函数y=﹣ ![]() x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y= ![]() 的图象在第一象限经过点A.
的图象在第一象限经过点A.
(1)求点A的坐标以及k的值:
(2)点P是反比例函数y= ![]() (x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
【答案】
(1)
解:由题可得:C(3,0),D(0,4).
过A作AE⊥y轴于E,如图(1):
在△AED和△DOC中,  ,
,
∴△AED≌△DOC,
∴AE=DO=4,ED=OC=3,
∴A点坐标为(4,7),
∵点A在反比例函数y= ![]() 的图象上,
的图象上,
∴k=28
(2)
解:设点P坐标为(x, ![]() ),
),
①当点P在OA上方时,如图(2):

过P作PG⊥y轴于G,过A作AF⊥y轴于F,
∵S△APO+S△PGO=S四边形PGFA+S△AFO,S△PGO=S△AFO=14,
∴S△APO=S四边形PGFA,
有: ![]() (x+4)(
(x+4)( ![]() ﹣7)=21,
﹣7)=21,
解得:x1=﹣8(舍去),x2=2;
即点P的坐标为(2,14);
②当点P在OA下方时,如图(3):

过P作PH⊥x轴于H,过A作AM⊥x轴于M,
∵S△APO+S△PHO=S四边形PHMA+S△AMO,S△PHO=S△AMO=14,
∴S△APO=S四边形PHMA,
有: ![]() (
( ![]() +7)(x﹣4)=21,
+7)(x﹣4)=21,
解得:x3=﹣2(舍去),x4=8,
即点P坐标为(8, ![]() ).
).
综上可知:当点P坐标为(2,14)或(8, ![]() )时,△PAO的面积为21
)时,△PAO的面积为21
【解析】(1)过点A作AE⊥y轴于E,证明△AED≌△DOC,可得点A坐标,代入求解即可;(2)分两种情况讨论:①点P在OA上方时,过P作PG⊥y轴于G,过A作AF⊥y轴于F,通过得出S△APO=S四边形PGFA , 可得点P坐标;②点P在OA下方时,过P作PH⊥x轴于H,过A作AM⊥x轴于M,通过S△APO=S四边形PHMA , 可得点P坐标.
【考点精析】掌握反比例函数的概念和反比例函数的图象是解答本题的根本,需要知道形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数y= ![]() (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动 
(1)若动点M、N同时出发,经过几秒钟两点相遇?
(2)若点E在线段BC上,BE=2cm,动点M、N同时出发且相遇时均停止运动,那么点M运动到第几秒钟时,与点A、E、M、N恰好能组成平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是36千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.求小明走路线一时的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项,现将调查结果绘制成如下所示的两幅统计图. 
请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)若该校八年级共有300名学生,请你估计其中最喜欢排球的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com