
【题目】在同一坐标系中,正比例函数y=x与反比例函数 ![]() 的图象大致是( )
的图象大致是( )
A.
B.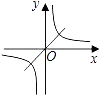
C.
D.
【答案】B
【解析】解:∵正比例函数y=x中,k=1>0, ∴此图象过一、三象限;
∵反比例函数 ![]() 中,k=2>0,
中,k=2>0,
∴此函数图象在一、三象限.
故选:B.
【考点精析】关于本题考查的一次函数的图象和性质和反比例函数的图象,需要了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):10、6、9、11、8、10,下列关于这组数据描述正确的是( )
A.极差是6
B.众数是10
C.平均数是9.5
D.方差是16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A. 
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣ ![]() x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y= ![]() 的图象在第一象限经过点A.
的图象在第一象限经过点A.
(1)求点A的坐标以及k的值:
(2)点P是反比例函数y= ![]() (x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF. 
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E. 
(1)若∠A+∠CDB=90°,求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A.![]()
B.![]()
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲、乙两个家庭有了各自的规划,假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com