
【题目】如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 . 
【答案】![]() ﹣1
﹣1
【解析】解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,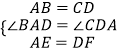 ,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,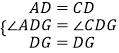 ,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO= ![]() AB=1,
AB=1,
在Rt△AOD中,OD= ![]() =
= ![]() =
= ![]() ,
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD﹣OH= ![]() ﹣1.
﹣1.
(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆 ![]() 上运动当O、H、D三点共线时,DH长度最小)
上运动当O、H、D三点共线时,DH长度最小)
所以答案是: ![]() ﹣1.
﹣1.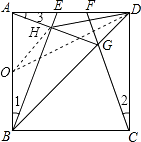
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)如图①,将矩形纸片沿AN折叠,点B落在对角线AC上的点E处,求BN的长;
(2)如图②,点M为AB上一点,将△BCM沿CM翻折至△ECM,ME与AD相交于点G,CE与AD相交于点F,且AG=GE,求BM的长;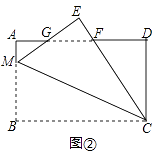
(3)如图③,将矩形纸片ABCD折叠,使顶点B落在AD边上的点E处,折痕所在直线同时经过AB、BC(包括端点),设DE=x,请直接写出x的取值范围: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A. 
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E、F分别是对角线BD上的两点,且BE=DF,连接AE、AF、CE、CF.四边形AECF是什么样的四边形,说明你的道理. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣ ![]() x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图象与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y= ![]() 的图象在第一象限经过点A.
的图象在第一象限经过点A.
(1)求点A的坐标以及k的值:
(2)点P是反比例函数y= ![]() (x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图象上一点,且△PAO的面积为21,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF. 
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com