
【题目】某地区为绿化环境,计划购买甲、乙两种树苗共计n棵.有关甲、乙两种树苗的信息如图所示:

(1)当n=400时,如果购买甲、乙两种树苗共用27000元,那么甲、乙两种树苗各买了多少棵?
(2)实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了m棵.
①写出m与n满足的关系式;
②要使这批树苗的成活率不低于92%,求n的最大值.
【答案】(1)甲种树苗300棵,乙种树苗100棵;(2)①m=3n-900;②n的最大值为375
【解析】分析:(1)、设甲种树苗的数量为x棵,则乙种树苗的数量为400-x棵,根据购买甲、乙两种树苗共用27000元可列方程求解即可;(2)、①根据总费用为27000元可列方程,得出m和n的函数关系式;②根据这批树苗的成活率不低于92%可列出不等式求解.
详解:(1)设甲种树苗的数量为x棵,则乙种树苗的数量为400-x棵,
60x+90(400-x)=27000, 解得x=300, 400-x=100.
答:甲种树苗买了300棵,乙种树苗买了100棵.
(2)①60m+90(n-m)=27000,即m=3n-900;
②90%m+95%(n-m)≥92%n, ∴3n-5m≥0, ∴3n-5(3n-900)≥0
∴n≤375, ∴n的最大值为375.


科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ; (2) (x–2)2–(x+2)(x–2)
; (2) (x–2)2–(x+2)(x–2)
解方程组:(3)![]() (4)
(4)
(5)化简求值 (m-n)2-2(m2-n2)+(m+n)2.(其中m=2018,n= -![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:

(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)请你设计一种方案,不仅每小时支付的租金最少,又恰好能完成每小时的挖掘量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
利用网格点和三角板画图或计算:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为( )
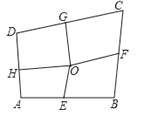
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年夏季,湖南省部分地区发生了罕见的旱灾,连续几个月无有效降水.为抗旱救灾,驻湘某部计划为驻地村民新建水渠3600米,为使水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.求实际每天修水渠多少米?(列方程解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
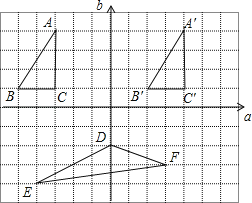
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com