
【题目】如图, ![]() ,且
,且![]() ,直线
,直线![]() 经过点
经过点![]() .设
.设![]() ,
,![]() 于点
于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
(1)当![]() 时,
时, ![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 的外心在其内部,直接写出
的外心在其内部,直接写出![]() 的取值范围.
的取值范围.
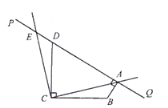
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;
(2)证明△ABC≌△EDC(AAS)即可求解;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.
解:(1)在四边形BADC中,∠B+∠ADC=360°-∠BAD-∠DCB=180°,
而∠ADC+∠EDC=180°,
∴∠ABC=∠PDC=α=125°,
故答案为125;
(2)如图,
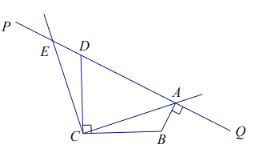
∵![]() ,又
,又![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到射线
得到射线![]() ,
,
∴![]() ,又
,又![]() ,
,
即![]() ,
,
在四边形![]() 中,
中,
![]()
∵![]()
∴![]()
又∵![]()
∴![]()
在![]() 和
和![]() 中,
中,
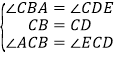 ,
,
∴![]()
∴![]()
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,
∠ABC=α>90°时,△ABC的外心在其外部,
而45°<α<135°,
故:45°<α<90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
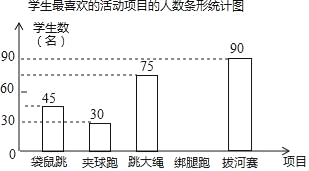
【题目】为了丰富校园文化,某校决定举行学生趣味运动会,将比赛项目确定为袋鼠跳,夹球跑,跳大绳,绑腿跑和拔河赛5项,为了解学生对这5项运动的喜欢情况,随机调查了该校部分学生最喜欢的一种项目(每名学生必选且只能选择5项中的一种),并将调查结果绘制成如图所示的不完整的统计图表:
根据图表中提供的信息解答下列问题:
(1)求a,b的值.
(2)请将条形统计图补充完整.
(3)根据调查结果,请你估计该校2500名学生中有多少名学生最喜欢绑腿跑.
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比(%) |
袋鼠跳 | 45 | 15 |
夹球跑 | a | 10 |
跳大绳 | 75 | 25 |
绑腿跑 | b | 20 |
拔河赛 | 90 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
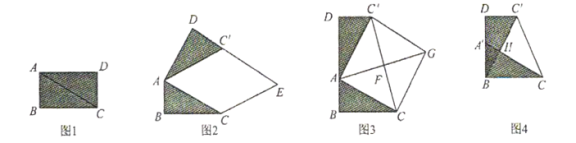
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练。王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的跳远成绩,将两次测得的成绩制作成图所示的统计图和不完整的统计表(满分10分,得分均为整数).
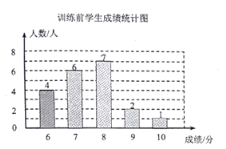
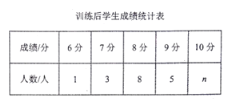
根据以上信息回答下列问题:
(1)训练后学生成绩统计表中![]() ,并补充完成下表:
,并补充完成下表:

(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?
(3)经调查,经过训练后得到9分的五名同学中,有三名男生和两名女生,王老师要从这五名同学中随机抽取两名同学写出训练报告,请用列表或画树状图的方法,求所抽取的两名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量为p时,其函数值等于p,则称p为这个函数的不变值,在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.
(1)判断函数y=![]() 有没有不变值?如果有,直接写出其不变长度.
有没有不变值?如果有,直接写出其不变长度.
(2)函数y=3x2-bx.
①若其不变长度为零,求b的值;
②若2≤b≤5,求其不变长度q的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=![]() ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用![]() 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
旋转是图形变化的方法之一,借助旋转知识可以解决线段长、角的大小、取值范围、判断三角形形状等问题,在实际生活中也有着十分重要的地位和作用.
问题背景
一块等边三角形建筑材料内一点到三角形三个顶点的距离满足一定条件时,我们可以用所学的知识帮助工人师傅在没有刻度尺的情况下求出等边三角形的边长.
数学建模
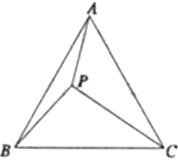
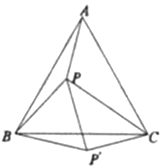
如图,等边三角形![]() 内有一点
内有一点![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
问题解决
(1)如图,将△ABP绕点![]() 顺时针旋转60°得到△CBP′,连接
顺时针旋转60°得到△CBP′,连接![]() ,易证∠BP′P=__°,△____为等边三角形,
,易证∠BP′P=__°,△____为等边三角形,![]() ____
____![]() ,
,![]() ___°.
___°.
(2)点H为直线BP′上的一个动点,则![]() 的最小值为______;
的最小值为______;
(3)求![]() 长;
长;
拓展延伸
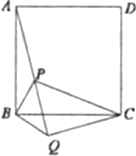
己知:点![]() 在正方形
在正方形![]() 内,点
内,点![]() 在平面内,
在平面内,![]() ,
,![]() .
.
(4)在图中,连接PA、PC、PQ、QC,![]() ,若点
,若点![]() 、
、![]() 、
、![]() 在一条直线上,则
在一条直线上,则![]() ____.
____.
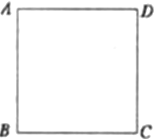
(5)若![]() ,连接
,连接![]() ,则______
,则______![]() ______;连接
______;连接![]() ,当
,当![]() 、
、![]() 、
、![]() 三点在同一条直线上时,△BDQ的面积为______.
三点在同一条直线上时,△BDQ的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com