
ЁОЬтФПЁПЖдгкФГвЛКЏЪ§ИјГіШчЯТЖЈвхЃКШєДцдкЪЕЪ§pЃЌЕБЦфздБфСПЮЊpЪБЃЌЦфКЏЪ§жЕЕШгкpЃЌдђГЦpЮЊетИіКЏЪ§ЕФВЛБфжЕЃЌдкКЏЪ§ДцдкВЛБфжЕЪБЃЌИУКЏЪ§ЕФзюДѓВЛБфжЕгызюаЁВЛБфжЕжЎВюqГЦЮЊетИіКЏЪ§ЕФВЛБфГЄЖШЃЎЬиБ№ЕиЃЌЕБКЏЪ§жЛгавЛИіВЛБфжЕЪБЃЌЦфВЛБфГЄЖШqЮЊСуЃЎ
(1)ХаЖЯКЏЪ§y=![]() гаУЛгаВЛБфжЕЃПШчЙћгаЃЌжБНгаДГіЦфВЛБфГЄЖШЃЎ
гаУЛгаВЛБфжЕЃПШчЙћгаЃЌжБНгаДГіЦфВЛБфГЄЖШЃЎ
(2)КЏЪ§y=3x2-bxЃЎ
ЂйШєЦфВЛБфГЄЖШЮЊСуЃЌЧѓbЕФжЕЃЛ
ЂкШє2ЁмbЁм5ЃЌЧѓЦфВЛБфГЄЖШqЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1)ВЛБфГЄЖШЮЊ4ЃЛ(2)Ђйb=-1ЃЛЂк1ЁмqЁм2ЃЎ
ЁОНтЮіЁП
(1)гаЃЎгЩЬтвтЕУЃКx=![]() x2ЃЌНтЕУЃКx=0Лђx=4ЃЛЕБx=0ЪБЃЌy=0ЃЌЕБx=4ЪБЃЌy=4ЃЌМДПЩЧѓНтЃЛ
x2ЃЌНтЕУЃКx=0Лђx=4ЃЛЕБx=0ЪБЃЌy=0ЃЌЕБx=4ЪБЃЌy=4ЃЌМДПЩЧѓНтЃЛ
(2)гЩЬтвтЕУЃКx=3x2-bxЃЌНтЕУЃКx=0Лђx=![]() ЃЌЂйМДЃКx=0Лђx=
ЃЌЂйМДЃКx=0Лђx=![]() ЪБЃЌЦфyжЕЯрЕШЃЌМДЃК0=
ЪБЃЌЦфyжЕЯрЕШЃЌМДЃК0=![]() ЃЌЙЪЃКb=-1ЃЛЂкЕБb=2ЪБЃЌx=0Лђx=1ЃЌдђЃКВЛБфГЄЖШq=1-0=1ЃЌЕБb=5ЪБЃЌx=0Лђx=2ЃЌдђq=2ЃЌМДПЩЧѓНтЃЎ
ЃЌЙЪЃКb=-1ЃЛЂкЕБb=2ЪБЃЌx=0Лђx=1ЃЌдђЃКВЛБфГЄЖШq=1-0=1ЃЌЕБb=5ЪБЃЌx=0Лђx=2ЃЌдђq=2ЃЌМДПЩЧѓНтЃЎ
НтЃК(1)гаЃЎгЩЬтвтЕУЃКx=![]() x2ЃЌНтЕУЃКx=0Лђx=4ЃЛ
x2ЃЌНтЕУЃКx=0Лђx=4ЃЛ
ЕБx=0ЪБЃЌy=0ЃЌЕБx=4ЪБЃЌy=4ЃЌ
ЙЪЃКВЛБфЃЌГЄЖШЮЊЃК4-0=4ЃЛ
(2)гЩЬтвтЕУЃКx=3x2-bxЃЌНтЕУЃКx=0Лђx=![]() ЃЌ
ЃЌ
ЂйМДЃКx=0Лђx=![]() ЪБЃЌЦфyжЕЯрЕШЃЌМДЃК0=
ЪБЃЌЦфyжЕЯрЕШЃЌМДЃК0=![]() ЃЌ
ЃЌ
ЙЪЃКb=-1ЃЛ
ЂкЕБb=2ЪБЃЌx=0Лђx=1ЃЌ
дђЃКВЛБфГЄЖШq=1-0=1ЃЌ
ЕБb=5ЪБЃЌx=0Лђx=2ЃЌдђq=2ЃЌ
ЙЪЃК1ЁмqЁм2ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЬсГіЃЉ|aЉ1|+|aЉ2|+|aЉ3|+Ё+|aЉ2019|зюаЁжЕЪЧЖрЩйЃП
ЃЈдФЖСРэНтЃЉ
ЮЊСЫНтОіетИіЮЪЬтЃЌЮвУЧЯШДгзюМђЕЅЕФЧщПіШыЪжЃЎ|a|ЕФМИКЮвтвхЪЧaетИіЪ§дкЪ§жсЩЯЖдгІЕФЕуЕНдЕуЕФОрРыЃЎФЧУД|aЉ1|ПЩвдПДзіaетИіЪ§дкЪ§жсЩЯЖдгІЕФЕуЕН1ЕФОрРыЃЛ|aЉ1|+|aЉ2|ОЭПЩвдПДзїaетИіЪ§дкЪ§жсЩЯЖдгІЕФЕуЕН1КЭ2СНИіЕуЕФОрРыжЎКЭЃЎЯТУцЮвУЧНсКЯЪ§жсбаОП|aЉ1|+|aЉ2|ЕФзюаЁжЕЃЎ
ЮвУЧЯШПДaБэЪОЕФЕуПЩФмЕФ3жжЧщПіЃЌШчЭМЫљЪОЃК
ЃЈ1ЃЉШчЭМЂйЃЌaдк1ЕФзѓБпЃЌДгЭМжаКмУїЯдПЩвдПДГіaЕН1КЭ2ЕФОрРыжЎКЭДѓгк1ЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌaдк1КЭ2жЎМфЃЈАќРЈдк1ЃЌ2ЩЯЃЉЃЌПЩвдПДГіaЕН1КЭ2ЕФОрРыжЎКЭЕШгк1ЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌaдк2ЕФгвБпЃЌДгЭМжаКмУїЯдПЩвдПДГіaЕН1КЭ2ЕФОрРыжЎКЭДѓгк1ЃЎ
ЃЈЮЪЬтНтОіЃЉ
ЃЈ1ЃЉ|aЉ2|+|aЉ5|ЕФМИКЮвтвхЪЧЁЁ ЁЁЃЎЧыФуНсКЯЪ§жсЬНОПЃК|aЉ2|+|aЉ5|ЕФзюаЁжЕЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉ|aЉ1|+|aЉ2|+|aЉ3|ЕФМИКЮвтвхЪЧЁЁ ЁЁЃЎЧыФуНсКЯЪ§жсЬНОПЃК|aЉ1|+|aЉ2|+|aЉ3|ЕФзюаЁжЕЪЧЁЁ ЁЁЃЌВЂдкЭМЂмЕФЪ§жсЩЯУшГіЕУЕНзюаЁжЕЪБaЫљдкЕФЮЛжУЃЌгЩДЫПЩвдЕУГіaЮЊЁЁ ЁЁЃЎ
ЃЈ3ЃЉЧѓГі|aЉ1|+|aЉ2|+|aЉ3|+|aЉ4|+|aЉ5|ЕФзюаЁжЕЃЎ
ЃЈ4ЃЉЧѓГі|aЉ1|+|aЉ2|+|aЉ3|+Ё+|aЉ2019|ЕФзюаЁжЕЃЎ
ЃЈЭиеЙгІгУЃЉ
ЧыдкЭМЂнЕФЪ§жсЩЯБэЪОГіaЃЌЪЙЫќЕН2ЃЌ5ЕФОрРыжЎКЭаЁгк4ЃЌВЂжБНгаДГіaЕФЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧЁАЙ§дВЩЯвЛЕузїдВЕФЧаЯпЁБЕФГпЙцзїЭМЙ§ГЬ.
вбжЊЃКЁбOКЭЁбOЩЯвЛЕуPЃЎ
ЧѓзїЃКЁбOЕФЧаЯпMNЃЌЪЙMNОЙ§ЕуPЃЎ

зїЗЈЃКШчЭМЃЌ
ЃЈ1ЃЉзїЩфЯпOPЃЛ
ЃЈ2ЃЉвдЕуPЮЊдВаФЃЌаЁгкOPЕФГЄЮЊАыОЖзїЛЁНЛЩфЯпOPгкAЃЌBСНЕуЃЛ
ЃЈ3ЃЉЗжБ№вдЕуAЃЌBЮЊдВаФЃЌвдДѓгк![]() ГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкMЃЌNСНЕуЃЛ
ГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкMЃЌNСНЕуЃЛ
ЃЈ4ЃЉзїжБЯпMN.дђMNОЭЪЧЫљЧѓзїЕФЁбOЕФЧаЯпЃЎ
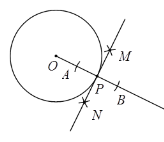
ЧыЛиД№ЃКИУГпЙцзїЭМЕФвРОнЪЧ____________________________________________________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1,Еу![]() КЭОиаЮ
КЭОиаЮ![]() ЕФБп
ЕФБп![]() ЖМдкжБЯп
ЖМдкжБЯп![]() ЩЯ,вдЕу
ЩЯ,вдЕу![]() ЮЊдВаФ,вд24ЮЊАыОЖзїАыдВ,ЗжБ№НЛжБЯп
ЮЊдВаФ,вд24ЮЊАыОЖзїАыдВ,ЗжБ№НЛжБЯп![]() гк
гк![]() СНЕу.вбжЊ:
СНЕу.вбжЊ: ![]() ,
,![]() ,ОиаЮздгвЯђзѓдкжБЯп
,ОиаЮздгвЯђзѓдкжБЯп![]() ЩЯЦНвЦ,ЕБЕу
ЩЯЦНвЦ,ЕБЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЪБ,ОиаЮЭЃжЙдЫЖЏ.дкЦНвЦЙ§ГЬжа,ЩшОиаЮЖдНЧЯп
ЪБ,ОиаЮЭЃжЙдЫЖЏ.дкЦНвЦЙ§ГЬжа,ЩшОиаЮЖдНЧЯп![]() гыАыдВ
гыАыдВ![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() (Еу
(Еу![]() ЮЊАыдВЩЯдЖРыЕу
ЮЊАыдВЩЯдЖРыЕу![]() ЕФНЛЕу).
ЕФНЛЕу).
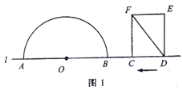
ЃЈ1ЃЉШчЭМ2ЃЌШє![]() гыАыдВ
гыАыдВ![]() ЯрЧаЃЌЧѓ
ЯрЧаЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
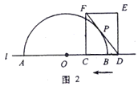
ЃЈ2ЃЉШчЭМ3ЃЌЕБ![]() гыАыдВ
гыАыдВ![]() гаСНИіНЛЕуЪБЃЌЧѓЯпЖЮ
гаСНИіНЛЕуЪБЃЌЧѓЯпЖЮ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
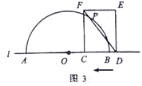
ЃЈ3ЃЉШєЯпЖЮ![]() ЕФГЄЮЊ20ЃЌжБНгаДГіДЫЪБ
ЕФГЄЮЊ20ЃЌжБНгаДГіДЫЪБ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
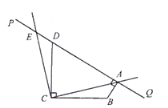
ЁОЬтФПЁПШчЭМ, ![]() ,Чв
,Чв![]() ,жБЯп
,жБЯп![]() ОЙ§Еу
ОЙ§Еу![]() .Щш
.Щш![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ,НЋЩфЯп
,НЋЩфЯп![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊ
АДФцЪБеыЗНЯђа§зЊ![]() ,гыжБЯп
,гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() .
.
(1)ЕБ![]() ЪБ,
ЪБ, ![]() ЃЛ
ЃЛ
(2)ЧѓжЄ: ![]() ЃЛ
ЃЛ
(3)Шє![]() ЕФЭтаФдкЦфФкВП,жБНгаДГі
ЕФЭтаФдкЦфФкВП,жБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцжБНЧзјБъЯЕжага5ИіЕуЃКAЃЈ1ЃЌ1ЃЉЃЌBЃЈЉ3ЃЌЉ1ЃЉЃЌCЃЈЉ3ЃЌ1ЃЉЃЌDЃЈЉ2ЃЎЉ2ЃЉЃЎ

ЃЈ1ЃЉЛГіЁїABCЕФЭтНгдВЁбPЃЌВЂжИГіЕуDгыЁбPЯрЕФЮЛжУЙиЯЕЃЛ
ЃЈ2ЃЉEЕуЪЧyжсЩЯЕФвЛЕуЃЌШєжБЯпDEгыЁбPЯрЧаЃЌЧѓЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫЙФРјОгУёНкдМгУЫЎЃЌВЩгУЗжЖЮМЦЗбЕФЗНЗЈАДдТМЦЫуУПЛЇМвЭЅЕФЫЎЗбЃЌдТгУЫЎСПВЛГЌЙ§20![]() ЪБЃЌАД2дЊЃЏ
ЪБЃЌАД2дЊЃЏ![]() МЦЗбЃЛдТгУЫЎСПГЌЙ§20
МЦЗбЃЛдТгУЫЎСПГЌЙ§20![]() ЪБЃЌЦфжаЕФ20
ЪБЃЌЦфжаЕФ20![]() ШдАД2дЊЃЏ
ШдАД2дЊЃЏ![]() ЪеЗбЃЌГЌЙ§ВПЗжАД
ЪеЗбЃЌГЌЙ§ВПЗжАД![]() дЊЃЏ
дЊЃЏ![]() МЦЗбЃЎЩшУПЛЇМвЭЅгУгУЫЎСПЮЊ
МЦЗбЃЎЩшУПЛЇМвЭЅгУгУЫЎСПЮЊ![]() ЪБЃЌгІНЛЫЎЗб
ЪБЃЌгІНЛЫЎЗб![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГі![]() КЭ
КЭ![]() ЪБ
ЪБ![]() гы
гы![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉаЁУїМвЕкЖўМОЖШНЛФЩЫЎЗбЕФЧщПіШчЯТЃК
дТЗн | ЫФдТЗн | ЮхдТЗн | СљдТЗн |
НЛЗбН№Жю | 30дЊ | 34дЊ | 42.6дЊ |
аЁУїМветИіМОЖШЙВгУЫЎЖрЩйСЂЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌQЪЧ![]() ЩЯвЛЖЈЕуЃЌPЪЧЯвABЩЯвЛЖЏЕуЃЌCЮЊAPжаЕуЃЌСЌНгCQЃЌЙ§ЕуPзї
ЩЯвЛЖЈЕуЃЌPЪЧЯвABЩЯвЛЖЏЕуЃЌCЮЊAPжаЕуЃЌСЌНгCQЃЌЙ§ЕуPзї![]() НЛ
НЛ![]() гкЕуDЃЌСЌНгADЃЌCDЃЎ
гкЕуDЃЌСЌНгADЃЌCDЃЎ
вбжЊ![]() ЃЌЩшAЃЌPСНЕуМфЕФОрРыЮЊ
ЃЌЩшAЃЌPСНЕуМфЕФОрРыЮЊ![]() ЃЌCЃЌDСНЕуМфЕФОрРыЮЊ
ЃЌCЃЌDСНЕуМфЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ЃЈЕБЕуPгыЕуAжиКЯЪБЃЌСюyЕФжЕЮЊ1.30ЃЉ
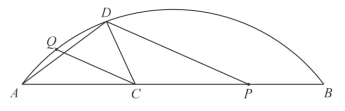
аЁШйИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНхГЃЎ
ЯТУцЪЧаЁШйЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫyгыxЕФМИзщЖдгІжЕЃК

ЃЈ2ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїзщЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ

ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБ![]() ЪБЃЌAPЕФГЄЖШдМЮЊ__________cmЃЎ
ЪБЃЌAPЕФГЄЖШдМЮЊ__________cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
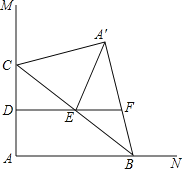
ЁОЬтФПЁПШчЭМЃЌЁЯMAN=90ЁуЃЌЕуCдкБпAMЩЯЃЌAC=4ЃЌЕуBЮЊБпANЩЯвЛЖЏЕуЃЌСЌНгBCЃЌЁїAЁфBCгыЁїABCЙигкBCЫљдкжБЯпЖдГЦЃЌЕуDЃЌEЗжБ№ЮЊACЃЌBCЕФжаЕуЃЌСЌНгDEВЂбгГЄНЛAЁфBЫљдкжБЯпгкЕуFЃЌСЌНгAЁфEЃЎЕБЁїAЁфEFЮЊжБНЧШ§НЧаЮЪБЃЌABЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com