
����Ŀ����̽����֪����ͼ1����C���߶�AB�ֳ�AC��BC�����֣���BC����AC����Ƶ�C���߶�AB��Բ���ʵ㣬�߶�AC��BC������ΪԲ���ʰ����߶Σ�
��1����AC��3����AB�� ��
��2������DҲ��ͼ1���߶�AB��Բ���ʵ㣨��ͬ��C�㣩����AC DB��

�������о�����ͼ2������һ��ֱ��Ϊ1����λ���ȵ�ԲƬ����ԲƬ�ϵ�ij���������ϱ�ʾ1�ĵ��غϣ�����ԲƬ���������������ع���1�ܣ��õ㵽���C��λ�ã�

��3������M��N��Ϊ�߶�OC��Բ���ʵ㣬���߶�MN�ij��ȣ�
��4��ͼ2�У�����D������OC�ϣ����߶�CD����O��C��D��ij������Ϊ�˵���߶λ�ΪԲ���ʰ����߶Σ���ֱ��д����D����ʾ������
���𰸡���1��3��+3����2��������3������1����4��1��������+![]() +2����2+2��+1��
+2����2+2��+1��
��������
��1�������߶�֮��Ĺ�ϵ�����ɣ�
��2�������߶εĴ�С�Ƚϼ��ɣ�
��3���������֪��C���ʾ��������+1����M����O�������OM=x�����ݳ��ȵĵ�����ϵ�г��������x����һ���õ��߶�MN�ij���.
��1����AC=3��BC=��AC��
��BC=3����
��AB=AC+BC=3��+3��
��2���ߵ�D��C�����߶�AB��Բ���ʵ��Ҳ��غϣ�
��BC=��AC��AD=��BD��
����AC=x��BD=y����BC=��x��AD=��y��
��AB=AC+BC=AD+BD��
��x+��x=y+��y��
��x=y
��AC=BD
��3���������֪��C���ʾ��������+1��
M��N��Ϊ�߶�OC��Բ���ʵ㣬������M����O�������OM=x��
x+��x=��+1�����x=1��
��MN=��+1-1-1=��-1��
��4�����D��ʾ����Ϊx��
��ͼ3����CD=��OD������+1-x=��x�����x=1��

��ͼ4����OD=��CD����x=������+1-x�������x=����

��ͼ5����OC=��CD������+1=����x-��-1�������x=��+![]() +2��
+2��

��ͼ6����CD=��OC����x-����+1��=������+1�������x=��2+2��+1��

���ϣ�D������ʾ������1��������+![]() +2����2+2��+1��
+2����2+2��+1��


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��ֱ��AB�ϵ�һ�㣬![]() ��ֱ�ǣ�OEƽ��
��ֱ�ǣ�OEƽ��![]() ��
��
��1����ͼ1����![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ1�У�![]() ��ֱ��д��
��ֱ��д��![]() �Ķ������ú�a�Ĵ���ʽ��ʾ����
�Ķ������ú�a�Ĵ���ʽ��ʾ����
��3����ͼ1�е�![]() �ƶ���O˳ʱ����ת��ͼ2��λ�ã�̽��
�ƶ���O˳ʱ����ת��ͼ2��λ�ã�̽��![]() ��
��![]() �Ķ���֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�
�Ķ���֮��Ĺ�ϵ��д����Ľ��ۣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������360�ֻ��ʣ�װ����6������3��С����������440�ֻ��ʣ�װ����8������2��С����
(1) ÿ������ÿ��С����ƽ����װ���ٶֻ��ʣ�
(2) �����ô���С����һ��10��ȥװ���ʣ�Ҫ����������������300�֣���������Ҫ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABC��������������Ϊ��A(1��4)��B(��3��3)��C(2����1)��������ABC����һ��P(m��n)����ƽ�ƺ�Ķ�Ӧ��ΪP1(m��3��n��2)����������ABC��ͬ��ƽ�Ƶõ�������A1B1C1.

��1����ͼ�л���������A1B1C1�� ��д��A1��B1��C1��������ꣻ
��2����������A1B1C1�������
��3������A��B��C��DΪ������ı�����ƽ���ı��Σ���ֱ��д����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�α���0��60���ȿ̶ȵ�������ƽ���۵����������ԣ���ʹ����������һ�����ص���Ȼ�����ص����������Ӵ�ֱ������ϣ������ӷ�ΪA��B��C���Σ��������εij����ɶ̵����ı�Ϊ1��2��3�����ۺ۶�Ӧ�Ŀ̶Ȳ������ǣ�������
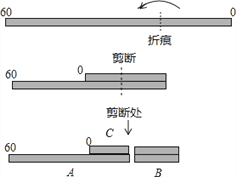
A. 20 B. 25 C. 30 D. 35
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����ֽƬABCD�У�AB��m��AD��n�������ű߳��ֱ�Ϊ8��6��������ֽƬ��ͼ1ͼ2���ַ�ʽ���ã�ͼ1��ͼ2������������ֽƬ���в����ص�������������δ��������������ֽƬ���ǵIJ�������Ӱ��ʾ����ͼ1����Ӱ���ֵ����ΪS1��ͼ2����Ӱ���ֵ����ΪS2��

��1�����ú�m��ʽ�ӱ�ʾͼ1��EF��BF�ij���
��2�����ú�m��n��ʽ�ӱ�ʾͼ1��ͼ2�е�S1��S2����m��n��3������S2��S1��ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����������ʽ��2��![]() ��22��2��
��22��2��![]() ��2��4��
��2��4��![]() ��42��2��
��42��2��![]() ��2�������������£����dz�ʹ��ʽab��a2��2b��2������һ��������a��bΪ��������������������Ϊ��a��b�����磺��2��
��2�������������£����dz�ʹ��ʽab��a2��2b��2������һ��������a��bΪ��������������������Ϊ��a��b�����磺��2��![]() ������4��
������4��![]() ������������������������
������������������������
��1���ж����ԣ���1����1���Ƿ�Ϊ��������������������˵�����ɣ�
��2������m��2������������������������6m��3[m2��2��2m��1��]��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O����AOE=90��.

��1����ͼ1����OCƽ�֡�AOE,���AOD�Ķ�����
��2����ͼ2������BOC=4��FOB����OEƽ�֡�FOC�����EOF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱߡ�ABC������B(0,0),C(2,0),�涨�ѡ�ABC����x�����ŵ�C˳ʱ����ת��ʹ��A����x���� ����Ϊһ�α任������x�����ŵ�A˳ʱ����ת��ʹ��B����x���� ����Ϊ���α任��������������2017�α任����A�������ǣ�

A. (4033�� ![]() ) B. (4033��0) C. (4036��
) B. (4033��0) C. (4036�� ![]() ) D. (4036��0)
) D. (4036��0)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com