
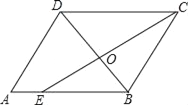
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.
科目:初中数学 来源: 题型:
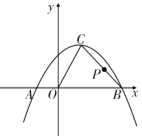
【题目】已知:如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)试确定该抛物线的函数表达式;
(2)已知点![]() 是该抛物线的顶点,求
是该抛物线的顶点,求![]() 的面积;
的面积;
(3)若点![]() 是线段
是线段![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形铁皮,长12dm,宽4dm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制作一个无盖方盒,如果要使制作的无盖方盒的侧面积.占矩形铁皮面积的八分之五,设各角切去的正方形的边长为xdm.
(1)用含x的代数式表示,盒底的长为______dm,盒底的宽为______dm;
(2)求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
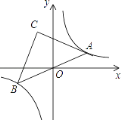
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走52米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.大楼AB的高度约为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
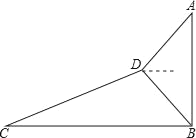
A. 32米B. 35米C. 36米D. 40米
查看答案和解析>>
科目:初中数学 来源: 题型:
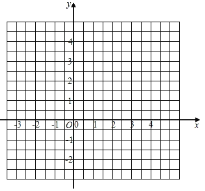
【题目】小明根据学习函数的经验,对函数y=![]() +1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)函数y=![]() +1的自变量x的取值范围是 ;
+1的自变量x的取值范围是 ;
(2)如表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x | … | ﹣ | ﹣1 | ﹣ | 0 |
|
| 2 |
| 3 |
| … |
y | … |
| m |
| 0 | ﹣1 | n | 2 |
|
|
| … |
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.
(4)结合函数的图象,解决问题:
①写出该函数的一条性质: .
②当函数值![]() +1>
+1>![]() 时,x的取值范围是: .
时,x的取值范围是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买![]() 两种型号的垃圾箱,通过市场调研得知:购买3个
两种型号的垃圾箱,通过市场调研得知:购买3个![]() 型垃圾箱和2个
型垃圾箱和2个![]() 型垃圾箱共需540元,购买2个
型垃圾箱共需540元,购买2个![]() 型垃圾箱比购买3个
型垃圾箱比购买3个![]() 型垃圾箱少用160元.
型垃圾箱少用160元.

(1)求每个![]() 型垃圾箱和
型垃圾箱和![]() 型垃圾箱各多少元?
型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买![]() 两种型号的垃圾箱共20个,则该小区最多可以购买
两种型号的垃圾箱共20个,则该小区最多可以购买![]() 型垃圾箱多少个.
型垃圾箱多少个.
查看答案和解析>>
科目:初中数学 来源: 题型:
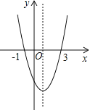
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com