
【题目】下列命题中,假命题的是( )
A. 四个角都相等的四边形是矩形
B. 两组对边分别相等的四边形是平行四边形
C. 对角线互相垂直且相等的四边形是正方形
D. 两条对角线互相垂直平分的四边形是菱形
科目:初中数学 来源: 题型:
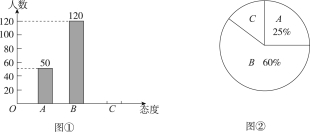
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者随机调查了某市城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成),并将调査结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中,共调査了 名中学生家长;
(2)将图①补充完整;
(3)根据抽样调查结果,请你估计该市城区80 000名中学生家长中有多少名家长持赞成态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点![]() .点
.点![]() 是原点,固定不动,点
是原点,固定不动,点![]() 和
和![]() 可以移动,点
可以移动,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .
.
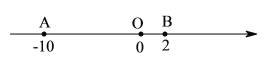
(1)点![]() 与点
与点![]() 之间的距离
之间的距离![]() _______.
_______.
(2)若![]() 点不动,点
点不动,点![]() 向右每秒移动
向右每秒移动![]() 个单位长,移动时间为
个单位长,移动时间为![]() 秒,此时点
秒,此时点![]() 与点
与点![]() 之间的距离
之间的距离![]() ________(用含
________(用含![]() 的代数式表示).
的代数式表示).
(3)若点![]() 向右每秒移动
向右每秒移动![]() 个单位长,点
个单位长,点![]() 同时向左每秒移动
同时向左每秒移动![]() 个单位长,设
个单位长,设![]() 为
为![]() 中点,当
中点,当![]() 相差
相差![]() 个单位长时,求
个单位长时,求![]() 点表示的数.
点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形土地上,修筑横向、纵向道路各一条,且它们互相垂直,若纵向道路的宽是横向道路的宽的2倍,要使剩余土地的面积为504平方米,求横向道路的宽为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南江县在“创国家级卫生城市”中,朝阳社区计划对某区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
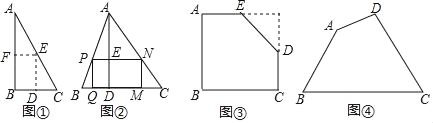
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
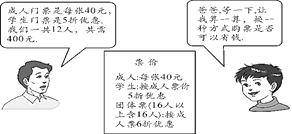
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com