
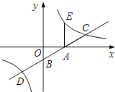
【题目】如图,直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与反比例函数
,与反比例函数![]() 图象交于点
图象交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②试判断点![]() 与点
与点![]() 是否关于原点
是否关于原点![]() 成中心对称?并说明理由.
成中心对称?并说明理由.
【答案】![]() 点
点![]() 的坐标为
的坐标为![]() ;②点
;②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.理由见解析.
成中心对称.理由见解析.
【解析】
(1)令一次函数中y=0,解关于x的一元一次方程,即可得出结论;
(2)①过点C作CF⊥x轴于点F,设AE=AC=t,由此表示出点E的坐标,利用特殊角的三角形函数值,通过计算可得出点C的坐标,再根据反比例函数图象上点的坐标特征可得出关于t的一元二次方程,解方程即可得出结论;
②根据点在直线上设出点D的坐标,根据反比例函数图象上点的坐标特征可得出关于点D横坐标的一元二次方程,解方程即可得出点D的坐标,结合①中点E的坐标即可得出结论.
![]() 当
当![]() 时,得
时,得![]() ,解得:
,解得:![]() .
.
∴点![]() 的坐标为
的坐标为![]() .:
.:![]() ①过点
①过点![]() 作
作![]() 轴于点
轴于点![]() ,如图所示.
,如图所示.
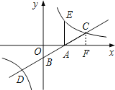
设![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
B(0,![]() )∴AB=3
)∴AB=3
∵![]()
∴![]()
∴![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]() .
.
②点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称,理由如下:
成中心对称,理由如下:
设点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
又∵点![]() 的坐标为
的坐标为![]() ,
,
∴点![]() 与点
与点![]() 关于原点
关于原点![]() 成中心对称.
成中心对称.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
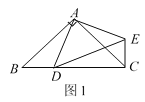
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
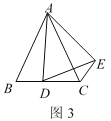
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应我市创建“全国文明城市”的号召,我区某校举办了一次“秀美巴中,绿色家园”主题演讲比赛,满分![]() 分,得分均为整数,成绩大于等于
分,得分均为整数,成绩大于等于![]() 分为合格,大于等于
分为合格,大于等于![]() 分为优秀,这次演讲比赛中甲、乙两组学生(各
分为优秀,这次演讲比赛中甲、乙两组学生(各![]() 名学生)成绩分布的条形统计图如下图:
名学生)成绩分布的条形统计图如下图:

(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 |
|
|
|
|
| |
乙 |
|
|
|
|
|
(2)小王同学说:“这次演讲赛我得了![]() 分,在我们小组中排名属中游略偏上!”观察上表可知,小王是________组的学生;(填“甲”或“乙”)
分,在我们小组中排名属中游略偏上!”观察上表可知,小王是________组的学生;(填“甲”或“乙”)
(3)结合两个小组的成绩分析,你觉得哪个组的成绩更好一些?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
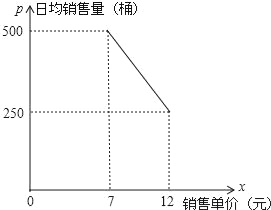
【题目】无锡市新区某桶装水经营部每天的房租、人员工资等固定成本为250元,每桶水的进价是5元,规定销售单价不得高于12元/桶,也不得低于7元/桶,调查发现日均销售量p(桶)与销售单价x(元)的函数图象如图所示.
(1)求日均销售量p(桶)与销售单价x(元)的函数关系;
(2)若该经营部希望日均获利1350元,那么销售单价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知反比例函数:y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是![]() 元,为了合理定价,投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,而销售单价每降低
件,而销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
件,但要求销售单价不得低于成本.求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com