
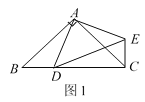
����Ŀ���ڡ�ABC�У�AB=AC����D��ֱ��BC��һ�㣨����B��C�غϣ�����ADΪһ����AD���Ҳ�����ADE��ʹAD=AE����DAE=��BAC������CE��
��1����ͼ1������D���߶�BC�ϣ������BAC=90�������BCE=_______�ȣ�
��2����ͼ2�����BAC=60�������BCE=______�ȣ�
��3�����BAC=![]() ����BCE=
����BCE=![]() ��
��
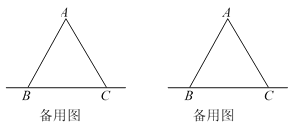
����ͼ3������D���߶�BC���ƶ�����![]() ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
�ڵ���D��ֱ��BC���ƶ�����ֱ��д��![]() ֮����������ϵ������֤����
֮����������ϵ������֤����

���𰸡���1��90����2��120�� ��3�� ����+��=180������+��=180������=��
��������
���⣨1����������֤����ABD�ա�ACE���ɵ���ABD=��ACE=45�㣬���������������ACB=45�㣬�������BCE=90�㣻
��2��ͬ��1����֤����ABD=��ACE������ABC���ɵ��������ε����ʿ������ACD���Ӷ��������BCE��
��3����ͬ��1����֤����ABD=��ACE������ABC���ɵ��������ε����ʿ������ACD=��ABC=![]() ���Ӷ��������BCE��������ͬ����
���Ӷ��������BCE��������ͬ����
�����������1���ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
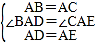
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=90�㣬
���ABD=��ACB=45�㣬
���BCE=��ACB+��ACE=45��+45��=90�㣬
��2���ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
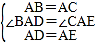
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=60�㣬
���ABD=��ACB=![]() =60�㣬
=60�㣬
���BCE=��ACB+��ACE=60��+60��=120�㣻
��3���١ߡ�DAE=��BAC��
���BAD=��CAE��
����ABD����ACE��
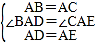
���ABD�ա�ACE��SAS����
���ABD=��ACE��
��AB=AC����BAC=����
���ABD=��ACB=![]() ��
��
���BCE=��ACB+��ACE=2��ACB=180��-����
����ͼ������D������BC��ʱ����+��=180��
��ͼ������D������BC�ķ����ӳ�����ʱ����=�£�



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������y1= ![]() ��x��0��ͼ���ϵ�����һ�㣬����A�� AB��x�ᣬ����һ����������y2=
��x��0��ͼ���ϵ�����һ�㣬����A�� AB��x�ᣬ����һ����������y2= ![]() ��k��0��x��0����ͼ���ڵ�B��
��k��0��x��0����ͼ���ڵ�B��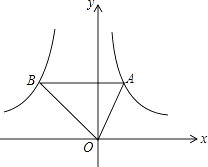
��1����S��AOB���������3����k��=��
��2����k=��8ʱ������A�ĺ�������1�����AOB�Ķ�����
��3�������۵�A�ںδ�������������y2= ![]() ��k��0��x��0��ͼ�����ܴ���һ��D��ʹ���ı���AOBDΪƽ���ı��Σ���k��ֵ��
��k��0��x��0��ͼ�����ܴ���һ��D��ʹ���ı���AOBDΪƽ���ı��Σ���k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
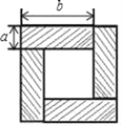
����Ŀ��(1)��ͼ����4��ȫ�ȵij�����ƴ�ɵ�һ�������Ρ������Σ�ͼ����Ӱ���������2�ַ�����ʾ�ɵ�һ����ʽ�������ʽΪ_______��
(2)��(4x��y)2=9��(4x+y)2=169����xy��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ��������M��a��b����N��c��d�����涨��a��b������c��d��=��a+c��b+d������Ƶ�Q��a+c��b+d��ΪM��N�ġ��͵㡱����������ԭ��O���������㼰���ǵġ��͵㡱Ϊ�����ܹ����ı��Σ��������ı���Ϊ���͵��ı��Ρ������е�A��2��5����B����1��3��������O��A��B��C�ĵ�Ϊ������ı����ǡ��͵��ı��Ρ������C�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���x2��x+a=0��ʵ����
��1����a��ȡֵ��Χ��
��2����x1��x2�Ƿ��̵�����ʵ�����������㣨x1+1����x2+1��=��1����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O���߶�AB��һ�㣬AB=4cm��AO=1cm�����߶�AB�Ƶ�O˳ʱ����ת120�㵽�߶�A��B���λ�ã����߶�AB����ת������ɨ����ͼ�ε����Ϊ cm2 �� ����������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Τκһ��������������ȥ��կ�����Σ����ϰ���;����֧������Ƴ������µ�ͳ��ͼ��
��1����һ���ֵķ���ռ����֧����![]() ��
��
��2�������ǹ����������8600Ԫ������ʳ������ȥ����Ԫ��
��3����һ��ס����·�ѹ�����Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�յ�Ǯ�����۳���Ϣ�����

��������Ϣ��С�콫�����泱���γɺ�ͷ���ҵ�֮��ľ��� ![]() ��ǧ�ף���ʱ��
��ǧ�ף���ʱ�� ![]() �����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11:40ʱ�ء����泱���ij�ͷ���ҵ�12ǧ�ס���Ϊ��
�����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11:40ʱ�ء����泱���ij�ͷ���ҵ�12ǧ�ס���Ϊ�� ![]() ����
���� ![]() ����Ϊ
����Ϊ ![]() ������
������ ![]() ���ö��κ���
���ö��κ��� ![]() ��
�� ![]() ��
�� ![]() �dz������̻���
�dz������̻���
��1���� ![]() ��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��2��11:59ʱ��С���ﵥ�����ҵس������ؽ��߹�·�� ![]() ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
��3��������С��������ת��ͷ���ؽ��߹�·����ͷ�ٶ��볱ͷ���У�����ͷ���ҵغ���ȼ��٣�����������ٶ�Ϊ ![]() ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�
ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ� ![]() ��
�� ![]() �Ǽ���ǰ���ٶȣ���
�Ǽ���ǰ���ٶȣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ƻ�����һЩ�ľ���ѧ����Ϊ��ѧУ����Χ�ơ��ڱʴ���Բ�桢ֱ�ߡ��ֱ������ľ��У�������Ҫ���ľ���ʲô������ѡ��ֻѡһ�֣��������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ���������������Ϣ�ش��������⣺
��1������ε����У�����ҪԲ���ѧ���ж�����������ȫ����ͳ��ͼ��
��2�����ȫУ��970��ѧ�����������ȫУѧ��������Ҫ�ֱʵ�ѧ���ж�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com