
【题目】如图,点A是反比例函数y1= ![]() (x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2=
(x>0)图象上的任意一点,过点A作 AB∥x轴,交另一个比例函数y2= ![]() (k<0,x<0)的图象于点B.
(k<0,x<0)的图象于点B.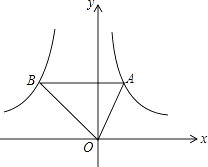
(1)若S△AOB的面积等于3,则k是=;
(2)当k=﹣8时,若点A的横坐标是1,求∠AOB的度数;
(3)若不论点A在何处,反比例函数y2= ![]() (k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
(k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
【答案】
(1)﹣4
(2)解:∵点A的横坐标是1,
∴y= ![]() =2,
=2,
∴点A(1,2),
∵AB∥x轴,
∴点B的纵坐标为2,
∴2=﹣ ![]() ,
,
解得:x=﹣4,
∴点B(﹣4,2),
∴AB=AC+BC=1+4=5,OA= ![]() =
= ![]() ,OB=
,OB= ![]() =2
=2 ![]() ,
,
∴OA2+OB2=AB2,
∴∠AOB=90°;
(3)解:假设y2= ![]() 上有一点D,使四边形AOBD为平行四边形,
上有一点D,使四边形AOBD为平行四边形,
过D作DE⊥AB,过A作AC⊥x轴,
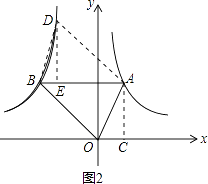
∵四边形AOBD为平行四边形,
∴BD=OA,BD∥OA,
∴∠DBA=∠OAB=∠AOC,
在△AOC和△DBE中,
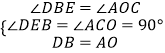 ,
,
∴△AOC≌△DBE(AAS),
设A(a, ![]() )(a>0),即OC=a,AC=
)(a>0),即OC=a,AC= ![]() ,
,
∴BE=OC=a,DE=AC= ![]() ,
,
∴D纵坐标为 ![]() ,B纵坐标为
,B纵坐标为 ![]() ,
,
∴D横坐标为 ![]() ,B横坐标为
,B横坐标为 ![]() ,
,
∴BE=| ![]() ﹣
﹣ ![]() |=a,即﹣
|=a,即﹣ ![]() =a,
=a,
∴k=﹣4.
【解析】解:如图1,设AB交y轴于点C,
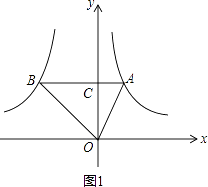
∵点A是反比例函数y1= ![]() (x>0)图象上的任意一点,且AB∥x轴,
(x>0)图象上的任意一点,且AB∥x轴,
∴AB⊥y轴,
∴S△AOC= ![]() ×2=1,
×2=1,
∵S△AOB=3,
∴S△BOC=2,
∴k=﹣4;
所以答案是:﹣4;
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:①甲车行驶40千米开始休息②乙车行驶3.5小时与甲车相遇③甲车比乙车晚2.5小时到到B地④两车相距50km时乙车行驶了![]() 小时,其中正确的说法有( )
小时,其中正确的说法有( )
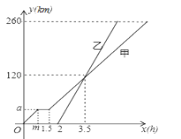
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
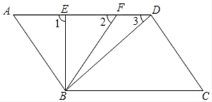
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形ABC,
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
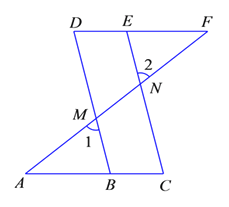
【题目】结合图形填空:已知:如图![]() ,
,![]() .求证:
.求证:![]() .
.
证明:∵![]() (已知),
(已知),
又![]() ( ),
( ),
∴![]() (等量代换),
(等量代换),
∴![]() (同位角相等,两直线平行),
(同位角相等,两直线平行),
∴![]() ( ).
( ).
∵![]() (已知),
(已知),
∴![]() (等量代换),
(等量代换),
∴![]() ( ),
( ),
∴![]() ( ).
( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() .给出下列三组条件(每组条件中的线段的长度已知):①
.给出下列三组条件(每组条件中的线段的长度已知):①![]() ,
,![]() ;②
;②![]() ,
,![]() ;③
;③![]() ,
,![]() ;能使
;能使![]() 唯一确定的条件的序号为( )
唯一确定的条件的序号为( )
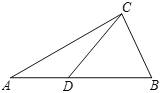
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
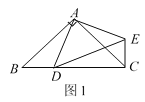
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
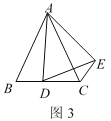
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com