
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
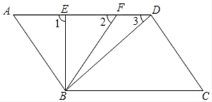
【题目】如图,已知AD∥BC,∠A=∠C=50°,线段AD上从左到右依次有两点E、F(不与A、D重合)
(1)AB与CD是什么位置关系,并说明理由;
(2)观察比较∠1、∠2、∠3的大小,并说明你的结论的正确性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度数,判断BE与AD是何种位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
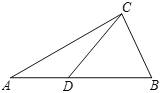
【题目】如图,![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() .给出下列三组条件(每组条件中的线段的长度已知):①
.给出下列三组条件(每组条件中的线段的长度已知):①![]() ,
,![]() ;②
;②![]() ,
,![]() ;③
;③![]() ,
,![]() ;能使
;能使![]() 唯一确定的条件的序号为( )
唯一确定的条件的序号为( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是一个无理数筛选器的工作流程图.
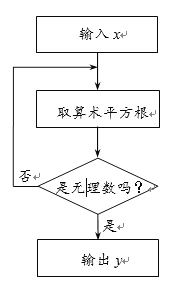
(1)当![]() 为16时,
为16时,![]() 值为 ;
值为 ;
(2)是否存在输入有意义的![]() 值后,却始终输不出
值后,却始终输不出![]() 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的![]() 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;
(3)如果输入![]() 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的![]() 值可能是什么情况;
值可能是什么情况;
(4)当输出的![]() 值是
值是![]() 时,判断输入的
时,判断输入的![]() 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )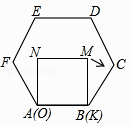
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
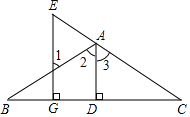
【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1,求证:AD平分∠ABC.下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC(已知)
∴∠ADC=∠EGC=90°( )
∴EG∥AD( )
∴∠E=________( )、
∠1=__________( )
又∵∠E=∠1(已知)
∴∠2=∠3( )
∴AD平分∠BAC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
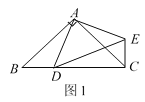
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
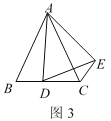
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
A(﹣1,1),B(﹣3,1),C(﹣1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).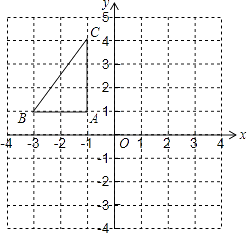
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图,不写作法,保留作图痕迹.
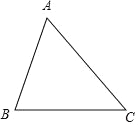
如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AB、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=15°,求∠BPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com