
【题目】如图,在直角坐标平面内有两点![]() 、
、![]() ,且
,且![]() 、
、![]() 两点之间的距离等于
两点之间的距离等于![]() (
(![]() 为大于0的已知数),在不计算
为大于0的已知数),在不计算![]() 的数值条件下,完成下列两题:
的数值条件下,完成下列两题:
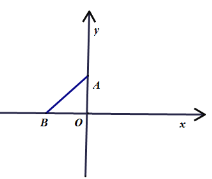
(1)以学过的知识用一句话说出![]() 的理由;
的理由;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是等腰三角形,如果存在,请写出点
是等腰三角形,如果存在,请写出点![]() 的坐标,并求
的坐标,并求![]() 的面积;如果不存在,请说明理由.
的面积;如果不存在,请说明理由.
【答案】(1)垂线段最短;(2)存在,当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() ;当
;当![]() ,
,![]() .
.
【解析】
(1)利用垂线段最短即可得出结论;
(2)分类讨论,利用等腰三角形的判定可得出P点坐标,利用三角形面积公式得出结论.
解:(1)∵在平面直角坐标系中,AO⊥BO,O为垂足,
∴AO表示A点到直线BO的距离,
∵![]() ,
,
∴![]() ,
,
∵垂线段最短,且![]() 不与O重合,
不与O重合,
∴![]() ,即
,即![]() ,
,
∴![]() 的理由是“垂线段最短”;
的理由是“垂线段最短”;
(2)在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
①如图1,当P在B点左边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
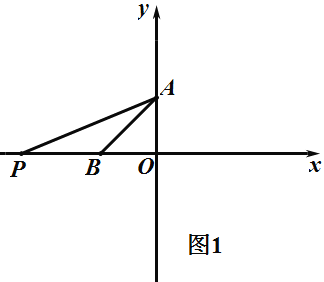
②如图2,当P在B点右边,BP=BA=a,![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
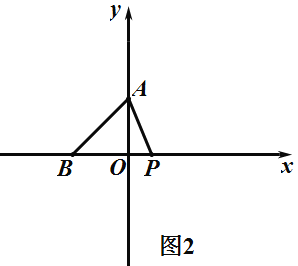
③如图3,当P在B点右边,BP=AP,![]() 为等腰三角形,
为等腰三角形,
此时P与O重合,即![]() ,
,
∵![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
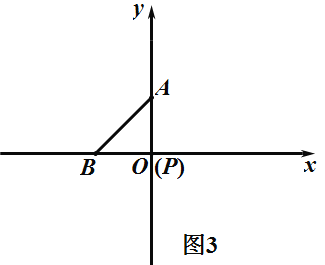
④如图4,当P在B点右边,AP=AB=a,![]() 为等腰三角形,
为等腰三角形,
∵AO⊥BO,
∴O为PB中点,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;

综上所述:在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 是等腰三角形,
是等腰三角形,
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;
当![]() ,
,![]() ;
;


科目:初中数学 来源: 题型:
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是 ![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线 ![]() 和线段
和线段 ![]() 分别表示两人离学校的路程
分别表示两人离学校的路程 ![]() (千米)与所经过的 时间
(千米)与所经过的 时间 ![]() (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程 ![]() (千米)与所经过的时间
(千米)与所经过的时间 ![]() (分钟)之间的函数表达式;
(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过 ![]() 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.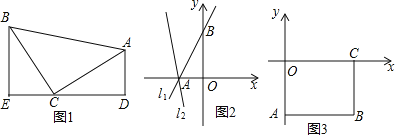
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A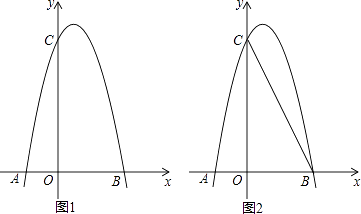
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决提出的问题:
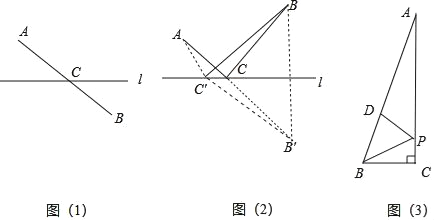
最短路径问题:如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B,这时对于直线l上的任一点C,都保持CB=CB,从而把问题(2)变为问题(1).因此,线段AB与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′.因为AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任务:
数学思考
(1)材料中划线部分的依据是 .
(2)材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)
A.转化思想
B.分类讨论思想
C.整体思想
迁移应用
(3)如图,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=8cm,则BP+DP的最小值为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.
![]()
(1)写出数轴上点B表示的数;
(2)若点M、N分别是线段AO、BO的中点,求线段MN的长;
(3)若动点P从点A出发.以每秒5个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.问点P运动多少秒时追上点Q?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅负责修理我校课桌椅,现知道李师傅修理2张课桌和3把椅子共需86分钟,修理5张课桌和2把椅子共需149分钟.
(1)请问李师傅修理1张课桌和1把椅子各需多少分钟
(2)现我校有12张课桌和14把椅子需要修理,要求1天做完,李师傅每天工作8小时,请问李师傅能在上班时间内修完吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D. 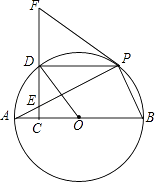
(1)证明:FP是⊙O的切线;
(2)若四边形OBPD是菱形,证明:FD=ED.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com