
����Ŀ���Ķ�����㣺���Ķ����²��ϣ��������Ӧ������
쳲�������Լ1170��1250�����������ѧ�ң����о���һ�������������dz��������Ϊ쳲��������У�����һ��˳�������ŵ�һ������Ϊ���У��������������о����Ĺ����У��������������벻���Ľ������ʵ�������У��ܶ�䣨��÷��������ݡ����پյȣ��İ���ǡ��쳲����������е�����쳲��������л��кܶ���Ȥ�����ʣ���ʵ��������Ҳ�й㷺��Ӧ�ã�쳲����������еĵ�n����������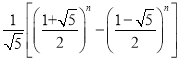 ��ʾ�����У�n��1������������������ʾ��������һ��������
��ʾ�����У�n��1������������������ʾ��������һ��������

������������ϲ��ϣ�ͨ���������쳲����������еĵ�1�����͵�2������
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=1��BC=2��BC��x���ϣ�һ�κ���y=kx��2��ͼ����A��C������y�ύ�ڵ�E������������y= ![]() ��ͼ����A��
��ͼ����A��
��1����E����������
��2�����������Ľ���ʽ��
��3����һ�κ�����ֵС�ڷ�����������ֵʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͯ������Ʊ�۸�涨���±���
��Ʊ���� | 1��50�� | 51��100�� | 100������ |
ÿ��Ʊ�ļ۸� | 13Ԫ | 11Ԫ | 9Ԫ |
ijУ���꼶��1������2�������102�˽���6.1��ͯ��ȥ�θ����������У�1�����������٣�����50�ˡ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ��1218Ԫ���ʣ�
��1����������ж���ѧ����
��2���������������������Ϊһ�����幺Ʊ�����Խ�ʡ����Ǯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���㣺
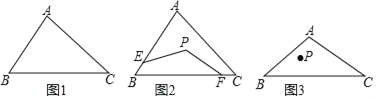
(1)��֪��ABC�����ó߹���ͼ1�С�ABC��ȷ��һ����P��ʹ�õ�P��AB��BC�ľ�����ȣ�������P����B�͵�C�ľ������(��д������������ͼ�ۼ�)��
(2)��ͼ2�������P��(1)�������ĵ㣬��E��F�ֱ��ڱ�AB��BC�ϣ���PE��PF��
������ABC��60�㣬���EPF�Ķ�����
����BE��2��BF��8��EP��5����BP�ij���
(3)��ͼ3�������P�ǡ�ABC��һ�㣬�ҵ�P����B�ľ�����7������ABC��45�㣬��ֱ���AB��BC������������M��N��ʹ�á�PMN���ܳ���С(��д������������ͼ�ۼ�)�����PMN����СֵΪ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD��EF�ֱ�AB��CD��G��F���㣬����FMƽ�֡�EFD��������FMƽ�ƣ�ʹ�ö˵�F���G�غ��ҵõ�����GN������EFC=110�������AGN�Ķ����ǣ�������

A. 120�� B. 125�� C. 135�� D. 145��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y1=k1x+b��ͼ����x�ᡢy��ֱ���A��B���㣬�뷴��������y2=![]() ��ͼ��ֱ���C��D���㣬��D��2����3������B���߶�AD���е㣮
��ͼ��ֱ���C��D���㣬��D��2����3������B���߶�AD���е㣮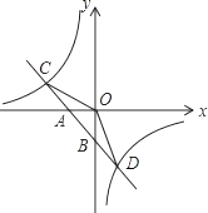
��1����һ�κ���y1=k1x+b�뷴��������y2=![]() �Ľ���ʽ��
�Ľ���ʽ��
��2�����COD�������
��3��ֱ��д�� k1x+b![]() ��0 ʱ�Ա���x��ȡֵ��Χ��
��0 ʱ�Ա���x��ȡֵ��Χ��
��4������P��0��m����y�����˶����� |PCPD| ��ֵ���ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��DΪ��ABC�ı�AB���ӳ�����һ�㣬��D��DF��AC������ΪF����BC��E,��BD=BE,��֤����ABC�ǵ���������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������ABC �У�AB=AC����BAC=90�㣬D ��BC ��һ�㣬EC��BC��EC=BD��DF=FE��

��֤����1����ABD�ա�ACE��
��2��AF��DE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������ж�������ֱ��ƽ�У���˵�����ݣ�

(1)��1=��2��________________________��
(2)��A=��3��________________________��
(3)��ABC+��C=180�㣬________________________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com