
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.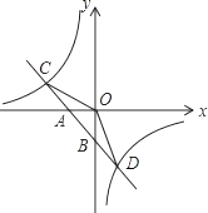
(1)求一次函数y1=k1x+b与反比例函数y2=![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出 k1x+b![]() ≥0 时自变量x的取值范围.
≥0 时自变量x的取值范围.
(4)动点P(0,m)在y轴上运动,当 |PCPD| 的值最大时,求点P的坐标.
【答案】
(1)解:∵点D(2,-3)在反比例函数y2=![]() 的图象上,
的图象上,
∴k2=2×(-3)=-6,
∴y2=![]() .
.
作DE⊥x轴于E,
∵D(2,-3),点B是AD的中点,
∴A(-2,0),
∵A(-2,0),D(2,-3)在y1=k1x+b的图象上,
∴![]() ,
,
∴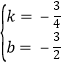
∴y1=-![]() x
x![]() .
.
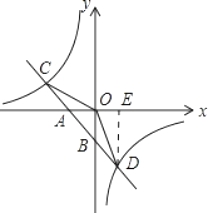
(2)解:依题可得: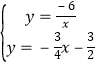 ,
,
∴C(-4, ![]() ),
),
∴S△COD=S△AOC+S△AOD
=![]() ·AO ·yC+
·AO ·yC+![]() ·AO·|yD|
·AO·|yD|
=![]() ×2×(
×2×(![]() +3)
+3)
=![]() .
.
(3)解:当x<-4或0<x<2时,y1>y2.
(4)解:C(-4,![]() )关于y轴的对称点C′(4,
)关于y轴的对称点C′(4,![]() ),延长C′D交y轴于点P,
),延长C′D交y轴于点P,
∵D(2,-3),
设直线C′D解析式为:y=cx+d,
∴![]()
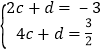 ,
,
∴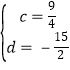 ,
,
∴直线C′D为 y=![]() x
x![]() ,
,
∴点P的坐标 为:(0, ![]() ).
).
【解析】(1)将D(2,-3)代入反比例函数y2=![]() ,即可求出k2的值,从而球场反比例函数解析式;作DE⊥x轴于E,由D(2,-3),点B是AD中点得出A(-2,0),将A(-2,0),D(2,-3)坐标代入y1=k1xb,得到一个二元一次方程组,解之即可得出一次函数解析式.
,即可求出k2的值,从而球场反比例函数解析式;作DE⊥x轴于E,由D(2,-3),点B是AD中点得出A(-2,0),将A(-2,0),D(2,-3)坐标代入y1=k1xb,得到一个二元一次方程组,解之即可得出一次函数解析式.
(2)将反比例函数和一次函数解析式联立即可得出C(-4, ![]() ),再由S△COD=S△AOC+S△AOD=
),再由S△COD=S△AOC+S△AOD=![]() ·AO ·yC+
·AO ·yC+![]() ·AO·|yD|,代入数值即可得出答案.
·AO·|yD|,代入数值即可得出答案.
(3)由图可得:当x<-4或0<x<2时,y1>y2.
(4)C(-4,![]() )关于y轴的对称点C′(4,
)关于y轴的对称点C′(4,![]() ),延长C′D交y轴于点,设直线C′D解析式为:y=cx+d,将C′和D点坐标代入得到一个二元一次方程组,解之即可得出直线C′D解析式,再令x=0即可求出点P的坐标.
),延长C′D交y轴于点,设直线C′D解析式为:y=cx+d,将C′和D点坐标代入得到一个二元一次方程组,解之即可得出直线C′D解析式,再令x=0即可求出点P的坐标.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).
①作出AD的依据是SAS;②∠ADC=60°
③点D在AB的中垂线上;④S△DAC:S△ABD=1:2.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用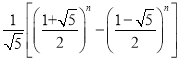 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.

任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分准备设计成若干个形状、大小完全相同的四边形图案,每平移一个图案,纹饰长度就增加![]() cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.
cm(如图)所示,已知每个四边形图案的水平方向的对角线长30cm.
(1)若![]() =26cm,且该纹饰要用231个四边形图案,求纹饰的长度
=26cm,且该纹饰要用231个四边形图案,求纹饰的长度![]() ;
;
(2)当![]() =20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?
=20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的四边形图案?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ A=500,∠C=700,BD、BE三等分∠ABC,将△BCE沿BE对折,点C落在C’处,则∠1=_________;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com