
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)﹣1,1,6;(2)-10;(3)BC﹣AB的值不变,BC﹣AB=4
【解析】试题分析:(1)根据最小的正整数是1,推出![]() 再利用非负数的性质求出
再利用非负数的性质求出![]() 即可.
即可.
(2)首先确定![]() 的范围,再化简绝对值即可.
的范围,再化简绝对值即可.
(3)![]() 的值不变.根据题意用
的值不变.根据题意用![]() 表示出
表示出![]() 即可解决问题.
即可解决问题.
试题解析:(1)∵b是最小的正整数,
∴b=1,
![]()
∴c=6,a=1,b=1,
故答案为1,1,6.
(2)由题意1<x<1,
∴|x+1||x1|2|x+5|=x+1+x12x10=10.
(3)不变,由题意BC=5+5nt2nt=5+3nt,AB=nt+1+2nt=1+3nt,
∴BCAB=(5+3nt)(1+3nt)=4,
∴BCAB的值不变,BCAB=4.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:![]()
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)试判断四边形AECF的形状;
(2)若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6 B. 6![]() C. 3
C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
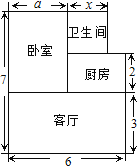
【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
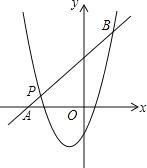
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014四川资阳)如图①,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧,满足BP=BE,连接AP,CE.
(1)求证:△ABP≌△CBE.
(2)连接AD、BD,BD与AP相交于点F,如图②.
①当![]() 时,求证:AP⊥BD;
时,求证:AP⊥BD;
②当![]() (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com