
【题目】(2014四川资阳)如图①,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2,l1于点D,E(点A,E位于点B的两侧,满足BP=BE,连接AP,CE.
(1)求证:△ABP≌△CBE.
(2)连接AD、BD,BD与AP相交于点F,如图②.
①当![]() 时,求证:AP⊥BD;
时,求证:AP⊥BD;
②当![]() (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求![]() 的值.
的值.

【答案】见解析
【解析】
(1)证明:BC⊥直线l1,
∴∠ABP=∠CBE.
在△ABP和△CBE中,
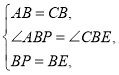
(2)①证明:如图,延长AP交CE于点H.
∵△ABP≌△CBE,
∴∠PAB=∠ECB,
∴∠PAB+∠AEH=∠ECB+∠AEH=90°,
∴∠AHE=90°,
∴AP⊥CE.
∵![]() ,即P为BC的中点,直线l1∥直线l2,
,即P为BC的中点,直线l1∥直线l2,
∴△CPD∽△BPE,
∴![]() ,
,
∴DP=EP.
∴四边形BDCE是平行四边形,∴CE∥BD.
∵AP⊥CE,∴AP⊥BD.
②解:∵![]() ,∴BC=nBP,
,∴BC=nBP,
∴CP=(n-1)BP.
∵CD∥BE,
∴△CPD∽△BPE,
∴![]() .
.
令S△BPE=S,则S2=(n-1)S,
S△PAB=S△BCE=nS,S△PAE=(n+1)S.
∵![]() ,
,
∴S1=(n+1)(n-1)S,
∴![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
![]()
(1)用“>”“<”或“=”填空:
b______0,a+b______0,a-c______0,b-c______0;
(2)化简:|c-a|-|c-b|+|a+b|.
查看答案和解析>>
科目:初中数学 来源: 题型:
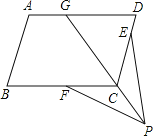
【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
求证:FP=EP.
查看答案和解析>>
科目:初中数学 来源: 题型:
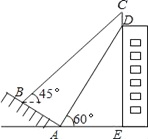
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,然后沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: ![]() (斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(1)求点B到地面的距离;
(2)求这块宣传牌CD的高度.(测角器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
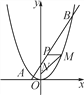
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() 与
与![]() 互为相反数.
互为相反数.
![]()
(1)![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数_________表示的点重合;
与数_________表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒2个单位长度的速度向左运动,同时,点
以每秒2个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒1个单位长度和3个单位长度的速度向右运动,假设
分别以每秒1个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请问:
,请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为32,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
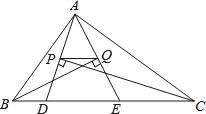
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式,例如![]() =1+
=1+![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ……这样的分式是假分式;像
……这样的分式是假分式;像![]() ,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:
,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:
![]()
![]()
(1)分式![]() 是 分式(填“真”或“假”);
是 分式(填“真”或“假”);
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com