
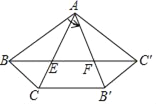
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A逆时针旋转α度(30<α<150)得到△AB′C′,B、C两点的对应点分别为点B′、C′,连接BC′,BC与AC、AB′相交于点E、F.
(1)当α=70时,∠ABC′=_____°,∠ACB′=______°.
(2)求证:BC′∥CB′.
【答案】(1)40,70;(2)证明见解析.
【解析】
(1)由旋转的性质可得AB=AC=AB'=AC',∠CAC'=70°,∠B'AC'=∠BAC=30°,由等腰三角形的性质可求解;
(2)由旋转的性质和等腰三角形的性质可得∠ABC'=![]() ,∠ACB'=
,∠ACB'=![]() ,由三角形的外角性质可得∠AEF=
,由三角形的外角性质可得∠AEF=![]() =∠ACB',即可得BC'∥CB'.
=∠ACB',即可得BC'∥CB'.
(1)∵将△ABC绕点A逆时针旋转α度得到△AB′C′,且AB=AC,∠BAC=30°,
∴AB=AC=AB'=AC',∠CAC'=70°,∠B'AC'=∠BAC=30°,
∴∠BAC'=100°,且AB=AC',
∴∠ABC'=40°,
∵∠CAB'=∠CAC'﹣∠B'AC'=40°,且AC=AB'
∴∠ACB'=70°
故答案为40,70
(2)∵将△ABC绕点A逆时针旋转α度得到△AB′C′,且AB=AC,∠BAC=30°,
∴AB=AC=AB'=AC',∠CAC'=α,∠B'AC'=∠BAC=30°,
∴∠BAC'=30°+α,∠CAB'=α﹣30°,且AB=AC=AB'=AC',
∴∠ABC'=![]() ,∠ACB'=
,∠ACB'=![]()
∵∠AEF=∠ABE+∠BAC
∴∠AEF=![]()
∴∠AEF=∠ACB',
∴BC'∥B'C


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
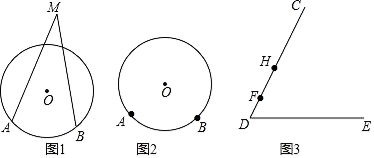
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某手机店1~4月的两张销售情况统计图,根据统计图,四个同学得出了以下四个结论,其中正确的为( )
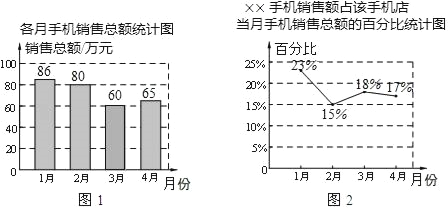
A. 4月××手机销售额为60万元
B. 4月××手机销售额比3月有所上升
C. 3月××手机销售额比2月有所上升
D. 3月与4月××手机的销售额无法比较,只能比较该店销售总额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,在横线上写出相应的函数关系式,并判断y是否为x的反比例函数(“是”就在后面的空格内打“1”,“不是”就在后面的空格内打“0”):
(1)长方形的面积S(cm2)一定,它的长y(cm)与宽x(cm)之间的关系式为 ________ .
(2)正方形的对角线长y(cm)与它的边长x(cm)之间的关系式为 ________ .
(3)一种商品的单价为a(元/件),所花费的钱数y(元)与购买的件数x(件)的关系式为 ________ .
(4)小明的家与学校相距2400m,他骑自行车上学的速度v(m/s)与所需时间t(s)的关系式为 ________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
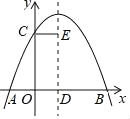
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E现有下列结论:①b2﹣4a<0;②b>0;③5a+b<0;④AD+CE=4.其中正确结论个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示。
销售量p(件) | P=50—x |
| 当1≤x≤20时, |
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数关系式。
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com