Question

2．我们把a、b中较小的数记作min{a，b}，设函数f（x）={2$\sqrt{x}$，|x-2|}．若动直线y=m与函数y=f（x）的图象有三个交点，它们的横坐标分别为x₁、x₂、x₃，则x₁x₂x₃的最大值为1．

Answer 1

分析 依照题意画出函数图象，并通过解方程组求出y=2$\sqrt{x}$与y=|x-2|的交点坐标，由此即可确定m的取值范围，不妨设x₁＜x₂＜x₃，将y=m分别代入y=2$\sqrt{x}$、y=2-x、y=x-2中求出x₁、x₂、x₃的值，将其相乘再根据完全平方公式即可解决最值问题．

解答 解：画出函数f（x）的图象，如图所示．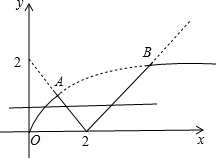
解方程组$\left\{\begin{array}{l}{y=2\sqrt{x}}\\{y=2-x}\end{array}\right.$和$\left\{\begin{array}{l}{y=2\sqrt{x}}\\{y=x-2}\end{array}\right.$得：$\left\{\begin{array}{l}{x=4-2\sqrt{3}}\\{y=2\sqrt{3}-2}\end{array}\right.$和$\left\{\begin{array}{l}{x=4+2\sqrt{3}}\\{y=2\sqrt{3}+2}\end{array}\right.$，
∴点A（4-2$\sqrt{3}$，2$\sqrt{3}$-2），点B（4+2$\sqrt{3}$，2$\sqrt{3}$+2），
∵动直线y=m与函数y=f（x）的图象有三个交点，
∴0＜m＜2$\sqrt{3}$-2．
不妨设x₁＜x₂＜x₃，
当y=2$\sqrt{x}$=m时，x₁=$\frac{{m}^{2}}{4}$；
当y=2-x=m时，x₂=2-m；
当y=x-2=m时，x₃=2+m．
∵0＜m＜2$\sqrt{3}$-2，
∴2-m＞0，2+m＞0，
∴x₁x₂x₃=$\frac{{m}^{2}}{4}$（2-m）（2+m）=$\frac{1}{4}$m²（4-m²）≤$\frac{1}{4}$$（\frac{{m}^{2}+4-{m}^{2}}{2}）^{2}$=1，
当且仅当m²=4-m²时，取等号，
∴m=$\sqrt{2}$时，x₁x₂x₃取最大值1．
故答案为：1．

点评 本题考查了一次函数的性质、函数图象以及完全平方公式，依照题意画出图形，利用数形结合找出m的取值范围是解题的关键．