

分析 (1)△ADF为直角三角形,有两种可能:∠ADF=90°或∠AFD=90°,根据锐角三角函数,分两种情况进行讨论,列方程求解即可;
(2)①根据菱形的判定,可知当AD=DF时,四边形ADFD′为菱形,根据锐角三角函数列方程求出x,计算菱形的面积即可;②根据三角形中位线定理可知,线段MN扫过的区域的形状是平行四边形,其面积为$\frac{24}{5}$.
解答 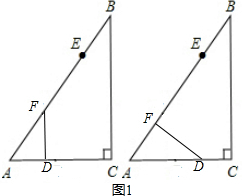 解:(1)∵∠ACB=90°,BC=8,tanA=$\frac{4}{3}$,
解:(1)∵∠ACB=90°,BC=8,tanA=$\frac{4}{3}$,
∴BC=8,AB=10,
∴AD=x,BE=x,AF=6-x,
当∠ADF=90°,如图1左图,
∵tanA=$\frac{4}{3}$,
∴cosA=$\frac{3}{5}$,
∴$\frac{AD}{AF}$=$\frac{x}{6-x}$=$\frac{3}{5}$,
∴x=$\frac{9}{4}$;
当∠AFD=90°,如图1右图,
∵tanA=$\frac{4}{3}$
∴cosA=$\frac{3}{5}$,
∴$\frac{AF}{AD}$=$\frac{6-x}{x}$=$\frac{3}{5}$,
∴x=$\frac{15}{4}$,
∴当x=$\frac{9}{4}$或$\frac{15}{4}$,△ADF为直角三角形;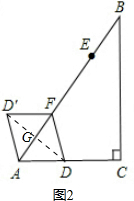 (2)①如图2,∵AD=AD′,D′F=DF,
(2)①如图2,∵AD=AD′,D′F=DF,
∴当AD=DF时,四边形ADFD′为菱形,
∴连接DD′⊥AF于G,AG=$\frac{6-x}{2}$,
∵tanA=$\frac{4}{3}$,
∴cosA=$\frac{3}{5}$,
∴$\frac{AG}{AD}$=$\frac{\frac{6-x}{2}}{x}$=$\frac{3}{5}$,
∴x=$\frac{30}{11}$,
∴S菱形=$\frac{1}{2}$×DD'×AF=$\frac{1}{2}$×$\frac{48}{11}$×$\frac{36}{11}$=$\frac{864}{121}$;
②平行四边形,$\frac{24}{5}$.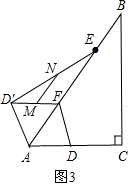
理由:如图3,∵M、N分别为D′F、D′E的中点,
∴MN∥EF,MN=$\frac{1}{2}$EF=2,
∴线段MN扫过的区域的形状是平行四边形,
当D运动到C,则F正好运动到A,此时MA=$\frac{1}{2}$D′A=$\frac{1}{2}$DA=3,
∵∠DAB=∠D′AB,
∴tanA=tan∠D′AB=$\frac{4}{3}$,
设点M到AB的距离为4x,则(3x)2+(4x)2=32,
解得:x=$\frac{3}{5}$,
∴4x=$\frac{12}{5}$,
∴线段MN扫过的区域的面积=2×$\frac{12}{5}$=$\frac{24}{5}$.
故答案为:平行四边形,$\frac{24}{5}$.
点评 本题属于四边形综合题,主要考查了锐角三角函数、直角三角形的判定、菱形的性质、勾股定理以及三角形中位线性质的综合运用,具备较强的数形结合能力是解决问题的关键.解题时注意分类讨论思想和方程思想的运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
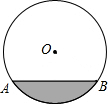 一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度.
一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com