
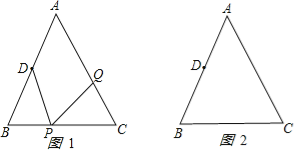
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
【答案】(1)全等,理由见解析;(2)![]() cm/s
cm/s
【解析】试题分析:(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等,则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
解:(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,
∵△ABC中,AB=AC,
∴在△BPD和△CQP中,
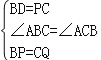 ,
,
∴△BPD≌△CQP(SAS).
(2)设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等;则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,
∵AB=AC,
∴∠B=∠C,
根据全等三角形的判定定理SAS可知,有两种情况:①当BD=PC,BP=CQ时,②当BD=CQ,BP=PC时,两三角形全等;
①当BD=PC且BP=CQ时,8﹣3t=5且3t=xt,解得x=3,∵x≠3,∴舍去此情况;
②BD=CQ,BP=PC时,5=xt且3t=8﹣3t,解得:x=![]() ;
;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A1B1C1 | A1(﹣3,2) | B1(﹣1,b) | C1(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在如图的平面直角坐标系中画出△ABC及△A1B1C1;
(3)△A1B1C1的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A. (x﹣1)2=4 B. (x+1)2=4 C. (x﹣1)2=16 D. (x+1)2=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚.

(1)任意转动转盘一次,获得猴年邮票的概率是 ;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
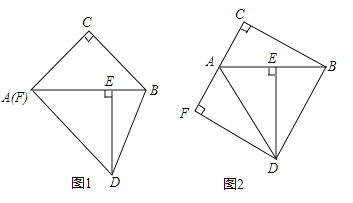
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
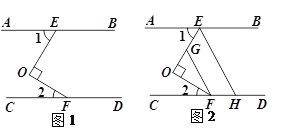
查看答案和解析>>
科目:初中数学 来源: 题型:
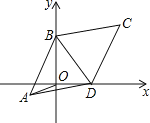
【题目】如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com