
分析 本题依据题中的等量关系:水稻2001年平均每公顷产7200kg,2003年平均每公顷产8460kg,根据增长后的产量=增长前的产量(1+增长率),设增长率是x,则2003年的产量是7200(1+x)2,据此即可列方程,解出后检验即可.
解答 解:设水稻每公顷产量的年平均增长率为x,
则有:7200(1+x)2=8460,
解得:x1≈0.084,x2=-=-2.084(不合题意舍去).
答:水稻每公顷产量的年平均增长率约为8.4%.
点评 本题考查了一元二次方程的应用,若原来的数量为a,平均每次增长或降低的百分率为x,经过第一次调整,就调整到a×(1±x),再经过第二次调整就是a×(1±x)(1±x)=a(1±x)2.增长用“+”,下降用“-”.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
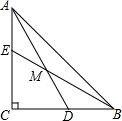 如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com