
科目:初中数学 来源: 题型:选择题
| A. | $\frac{800}{x+50}$=$\frac{600}{x}$ | B. | $\frac{800}{x-50}$=$\frac{600}{x}$ | C. | $\frac{800}{x}$=$\frac{600}{x+50}$ | D. | $\frac{800}{x}$=$\frac{600}{x-50}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
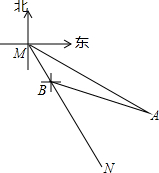 如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如图,东站枢纽建设要新建一条从M地到N地的公路,测得N点位于M点的南偏东30°,A点位于M点的南偏东60°,以A点为中心,半径为500米的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75°,量得MB=400米,请计算后回答公路是否会穿越文物保护区(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
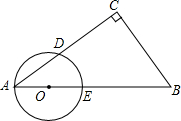 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com