
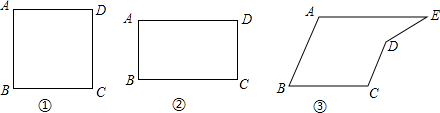
分析 (1)分别取BC、CD的三等分点E、F、G、H,作直线AF、AG即可;
(2)分别取BC、CD的三等分点E、F、G、H,作直线AF、AG即可;
(3)作AF⊥BC于F,延长CD交AE于G,由等腰三角形的性质得出BF=CF=$\frac{1}{2}$BC=60米,由勾股定理求出AF,证明四边形ABCG是平行四边形,求出平行四边形ABCG的面积,进一步求出五边形ABCDE的面积=平行四边形ABCG的面积+S△DGE,得出三等分图形的面积,再由三角形的面积关系得出点H、M是小路尽头的位置,作出直线即可.
解答 解 :(1)在正方形ABCD中,
:(1)在正方形ABCD中,
分别取BC、AD的三等分点E、F、G、H,
作直线EG、FH,
即把正方形ABCD的面积三等分;
如图1所示:
(2)在矩形ABCD中,
分别取BC、CD的三等分点E、F、G、H,
作直线AF、AG,
即把正方形ABCD的面积三等分;
如图2所示;
(3)作AF⊥BC于F,延长CD交AE于G,如图3所示:
∵AB=AC,
∴BF=CF=$\frac{1}{2}$BC=60米
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{10{0}^{2}-6{0}^{2}}$=80(米),
∵AB∥CD、AE∥BC,
∴四边形ABCG是平行四边形,
∴平行四边形ABCG的面积=BC•AF=120×80=9600(平方米),
∴CG=AB=100米,AG=BC=120米,DG=CG-CD=100-62.5=37.5(米),GE=AE-AG=160-120=40(米),
∴$\frac{DG}{CD}$=$\frac{37.5}{62.5}$=$\frac{3}{5}$,
∵AF=80米,
∴根据平行线截得的线段成比例:△DGE的GE边上的高为:30米,
∴S△DGE=$\frac{1}{2}$×30×40=600(平方米),
五边形ABCDE的面积=平行四边形ABCG的面积+S△DGE=9600+600=10200(平方米),
则三等分面积为3400平方米,
设在BC边上截取点H,使△ABH的面积为3400平方米,
即$\frac{1}{2}$AF•BH=3400,$\frac{1}{2}$×80BH=3400,
解得:BH=85(米),
∵S△ABC=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×120×80=4800(平方米),
∴S△ACH=S△ABC-S△ABH=4800-3400=1400(平方米),
∵S△ACD=480×$\frac{5}{8}$=300(平方米),140+200=340(平方米),
∴在CD上取CD的第二个三等分点M,CM=$\frac{2}{3}$CD=$\frac{125}{3}$(米),
∴直线AH、AM就可把五边形面积三等分,
∴H、M点就是小路尽头的位置.
点评 本题是面积及等积变换综合题目,考查了正方形的性质、矩形的性质、平行四边形的判定与性质、三角形面积的计算等知识;本题有一定难度,特别是(3)中,证明平行四边形进一步求出不规则的五边形ABCDE的面积是解决问题的突破口.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
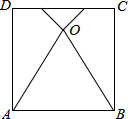 如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示)
如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
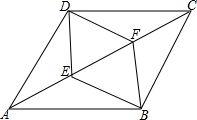 如图,?ABCD中,点E、F为对角线AC的三等分点,顺次连接点B、E、D、F.
如图,?ABCD中,点E、F为对角线AC的三等分点,顺次连接点B、E、D、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com