
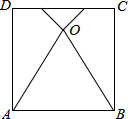
 如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示)
如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为(3+2$\sqrt{3}$)a.(用a的代数式表示) 分析 作OG⊥CD于G,交AB于H,根据翻转变换的性质得到OA=AD,OB=BC,∠EOA=∠D=90°,∠FOB=∠C=90°,根据直角三角形的性质和勾股定理求出DE、EF、FC,得到正方形的边长,计算即可.
解答 解:作OG⊥CD于G,交AB于H,
∵CD∥AB,
∴OH⊥AB于H,
由翻转变换的性质可知,OA=AD,OB=BC,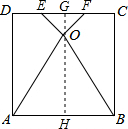 ∠EOA=∠D=90°,∠FOB=∠C=90°,
∠EOA=∠D=90°,∠FOB=∠C=90°,
∴△OAB是等边三角形,∠EOF=120°,
∴∠OEF=30°,
∴EO=2a,EG=$\sqrt{3}$a,
∴DE=OE=2a,OF=FC=2a,EF=2EG=2$\sqrt{3}$a,
∴DC=4a+2$\sqrt{3}$a,
∴点O到边AB的距离为4a+2$\sqrt{3}$a-a=3a+2$\sqrt{3}$a=(3+2$\sqrt{3}$)a.
故答案为:(3+2$\sqrt{3}$)a.
点评 本题考查的是翻转变换的性质和等边三角形的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:解答题
 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com