
【题目】如图,已知数轴上两点A,B对应的有理数分别为a,b,则A.B两点之间的距离是AB=![]() 或AB=
或AB=![]() 。回答下列问题:
。回答下列问题:
![]()
(1)数轴上表示2和9的两点之间的距离是 ;表示-3和8的两点之间的距离是 ;
(2)如果x和-2在数轴上对应点的距离是5,那么x= ;
(3)数轴上表示a和-3的两点之间的距离表示为 ;
(4)若数轴上表示a的点位于-3与2之间,则![]() ;
;
(5)当点P到-2和3对应的点A、B的距离之和为7时,则点P对应的数是 。
【答案】(1)7、11;(2)3或-7;(3)![]() 或
或![]() ;(4)5;(5)-3或4.
;(4)5;(5)-3或4.
【解析】
(1)根据数轴上两点间的距离公式代入求解即可;(2)根据题意列方程求解即可;(3)根据题意列出式子![]() 或
或![]() ;(4)根据点a的位置判断a+3与a-2的符号,再根据绝对值的定义去绝对值符号后化简即可;(5)根据题意列出方程
;(4)根据点a的位置判断a+3与a-2的符号,再根据绝对值的定义去绝对值符号后化简即可;(5)根据题意列出方程![]() ,再根据点P的位置分情况讨论求解.
,再根据点P的位置分情况讨论求解.
(1)数轴上表示2和9的两点之间的距离是![]() ;表示-3和8的两点之间的距离是
;表示-3和8的两点之间的距离是![]() ;
;
(2)∵x和-2在数轴上对应点的距离是5,∴![]() ,
,
∴![]() 或
或![]() ,∴
,∴![]() 或
或![]() ;
;
(3)数轴上表示a和-3的两点之间的距离表示为![]() 或
或![]() ;
;
(4)∵数轴上表示a的点位于-3与2之间,∴![]() ,
,![]() ,
,
∴|a+3|+|a-2|=a+3+(2-a)=5;
(5)设点P在数轴上对应的点为x,
∵点P到-2和3对应的点A、B的距离之和为7,
∴![]() ,
,
当点P在-2的左侧时,![]() ,解得x=-3;
,解得x=-3;
当点P在-2与3之间时,![]() ,无解;
,无解;
当点P在3的右侧时,![]() ,解得x=4;
,解得x=4;
综上P对应的数是-3或4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
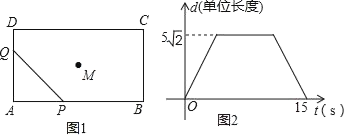
【题目】如图1已知矩形![]() ,
,![]() ,点
,点![]() 为矩形中心(
为矩形中心(![]() 与
与![]() 交点),现有两动点
交点),现有两动点![]() 分别沿着
分别沿着![]() 及
及![]() 的方向同时出发匀速运动,速度都为每秒一个单位长度,当点
的方向同时出发匀速运动,速度都为每秒一个单位长度,当点![]() 到达终点
到达终点![]() 时两动点都停止运动,连接
时两动点都停止运动,连接![]() ,在运动过程中,设运动时间为
,在运动过程中,设运动时间为![]() ,线段
,线段![]() 长度为
长度为![]() 个单位长度,
个单位长度,![]() 与
与![]() 的函数关系如图2
的函数关系如图2
(1)![]()
![]() .
.
(2)![]() 为多少时,线段
为多少时,线段![]() 经过点
经过点![]() ?并且求出此时
?并且求出此时![]() 的度数.
的度数.
(3)运动过程中,连接![]() 和
和![]() ,求当
,求当![]() 为直角时的
为直角时的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-5,
点对应的数为-5,![]() 点对应的数为55.现有一动点
点对应的数为55.现有一动点![]() 以6个单位/秒的速度从
以6个单位/秒的速度从![]() 点出发,同时另一动点
点出发,同时另一动点![]() 恰好以4个单位/秒的速度从
恰好以4个单位/秒的速度从![]() 点出发:
点出发:

(1)若![]() 向左运动,同时
向左运动,同时![]() 向右运动,在数轴上的
向右运动,在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(2)若![]() 向左运动,同时
向左运动,同时![]() 向左运动,在数轴上的
向左运动,在数轴上的![]() 点相遇,求
点相遇,求![]() 点对应的数.
点对应的数.
(3)若![]() 向左运动,同时
向左运动,同时![]() 向右运动,当
向右运动,当![]() 与
与![]() 之间的距离为20个单位长度时,求此时
之间的距离为20个单位长度时,求此时![]() 点所对应的数.
点所对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出了一个问题:
如图1,A、B两点被池塘隔开,在AB外选一点,连接AC和BC,怎样测出A、B两点的距离?

【活动探究】学生以小组展开讨论,总结出以下方法:
(1)如图2,选取点C,使AC=BC=a,∠C=60°;
(2)如图3,选取点C,使AC=BC=b,∠C=90°;
(3)如图4,选取点C,连接AC,BC,然后取AC、BC的中点D、E,量得DE=c…
【活动总结】
(1)请根据上述三种方法,依次写出A、B两点的距离.(用含字母的代数式表示)并写出方法(3)所根据的定理.
AB= ,AB= ![]() b ,AB= .
b ,AB= .
定理: .
(2)请你再设计一种测量方法,(图5)画出图形,简要说明过程及结果即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,左边是小颗的圆柱形笔筒,右边是小彬的六棱柱形笔筒,仔细观察两个笔简,并回答下面问题.

(1)圆柱、六棱柱各有几个面?
(2)圆柱的侧面与底面相交的线是直的还是曲的?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点(各写出一个)
查看答案和解析>>
科目:初中数学 来源: 题型:
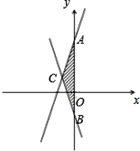
【题目】已知,直线 y=2x+3 与直线 y= ﹣ 2x ﹣ 1.
( 1 )求两直线与 y 轴交点A,B的坐标;
( 2 )求两直线交点 C 的坐标;
( 3 )求 △ ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG=![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A. 1
B. 2
C. 3
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题,求解下列各题:
(1)两个单项式![]() 与﹣5my﹣1n6是同类项,求解x和y;
与﹣5my﹣1n6是同类项,求解x和y;
(2)两个单项式m|3x﹣2|n|y+1|与2m4n6﹣|2y﹣1|是同类项,求解x和y;
(3)两个单项式mnax+ab与![]() 是同类项,求解x.
是同类项,求解x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com