
【题目】如图,左边是小颗的圆柱形笔筒,右边是小彬的六棱柱形笔筒,仔细观察两个笔简,并回答下面问题.

(1)圆柱、六棱柱各有几个面?
(2)圆柱的侧面与底面相交的线是直的还是曲的?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点(各写出一个)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在下列横线上用含有a,b的代数式表示相应图形的面积.
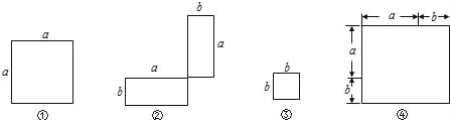
⑴① ② ③ ④
⑵通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系? 请用数学式子表示: ;
⑶利用(2)的结论计算:
①![]()
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
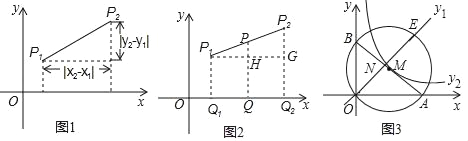
【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=![]() ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=![]() ,y=
,y=![]() .
.
启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S. S与t的部分函数图象如图2所示,已知点M(1,![]() )、N(5,6)在S与t的函数图象上.
)、N(5,6)在S与t的函数图象上.
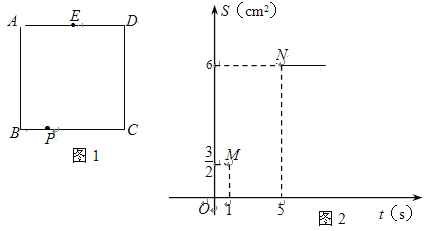
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图象;
(3)当t为多少时,△PBF的面积S为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)观察下列图形与等式的关系,并填空:
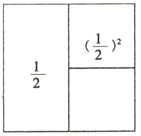
![]() +(
+(![]() )2=1﹣(
)2=1﹣(![]() )2;
)2;
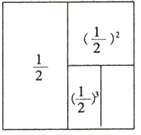
![]() +(
+(![]() )2+(
)2+(![]() )3=
)3=
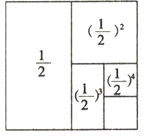
![]() +(
+(![]() )2+(
)2+(![]() )3+(
)3+(![]() )4=
)4=
(规律探究)观察下图:
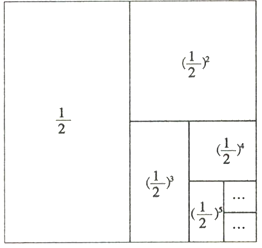
根据以上发现,用含n的代数式填空:![]() +(
+(![]() )2+(
)2+(![]() )3+(
)3+(![]() )4+(
)4+(![]() )5+…+(
)5+…+(![]() )n= .
)n= .
(解决问题)根据以上发现,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上两点A,B对应的有理数分别为a,b,则A.B两点之间的距离是AB=![]() 或AB=
或AB=![]() 。回答下列问题:
。回答下列问题:
![]()
(1)数轴上表示2和9的两点之间的距离是 ;表示-3和8的两点之间的距离是 ;
(2)如果x和-2在数轴上对应点的距离是5,那么x= ;
(3)数轴上表示a和-3的两点之间的距离表示为 ;
(4)若数轴上表示a的点位于-3与2之间,则![]() ;
;
(5)当点P到-2和3对应的点A、B的距离之和为7时,则点P对应的数是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件,可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排![]() 名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
名工人制造甲种零件,其余工人制造乙种零件,且生产乙种零件的个数不超过甲种零件个数的一半.
(1)请写出此车间每天所获利润![]() (元)与
(元)与![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)求自变量![]() 的取值范围;
的取值范围;
(3)怎样安排生产每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
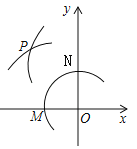
A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
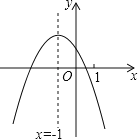
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com