
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2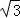 ;③tan∠DCF=
;③tan∠DCF=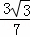 ;④△ABF的面积为
;④△ABF的面积为 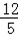
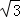 .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
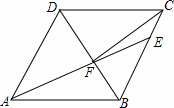
①②③
解:∵菱形ABCD,
∴AB=BC=6,
∵∠DAB=60°,
∴AB=AD=DB,∠ABD=∠DBC=60°,
在△ABF与△CBF中,
,
∴△ABF≌△CBF(SAS),
∴①正确;
过点E作EG⊥AB,过点F作MH⊥CD,MH⊥AB,如图:
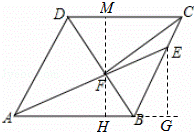
∵CE=2,BC=6,∠ABC=120°,
∴BE=6﹣2=4,
∵EG⊥AB,
∴EG= 2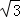 ,
,
∴点E到AB的距离是2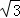 ,
,
故②正确;
∵BE=4,EC=2,
∴S△BFE:S△FEC=4:2=2:1,
∴S△ABF:S△FBE=3:2,
∴△ABF的面积为=  ,
,
故④错误;
∵∵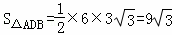 ,
,
∴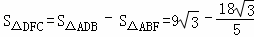 =
=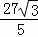 ,
,
∵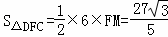 ,
,
∴FM=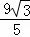 ,
,
∴DM=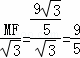 ,
,
∴CM=DC﹣DM=6﹣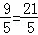 ,
,
∴tan∠DCF=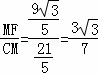 ,
,


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,△ABC的顶点都在方格纸的格点上,如果将△ABC先向右平移4个单位长度,在向下平移1个单位长度,得到△A1B1C1,那么点A的对应点A1的坐标为( )
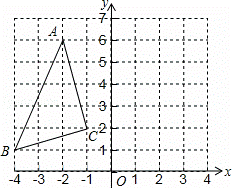
A. (4,3) B. (2,4) C. (3,1) D. (2,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
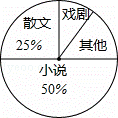
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”
四个类别,每位同学仅选一项,根 据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | m | 1 |
(1)计算m= 40 ;
(2)在扇形统计图中,“其他”类所占的百分比为 15% ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件发生的概率为0的是( )
A. 射击运动员只射击1次,就命中靶心
B. 任取一个实数x,都有 |x|≥0
|x|≥0
C. 画一个三角形,使其三边的长分别为8cm,6cm,2cm
D. 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com