
分析 (1)利用等边三角形的性质得:AC=MC,CN=BC,∠ACM=∠BCN=60°,证明△ACN≌△MCB,可以得出结论;
(2)根据正方形的性质证明△ACN≌△MCB,可以得结论.
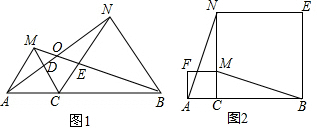
解答 证明:(1)如图1,∵△ACM、△BCN都是等边三角形,
∴AC=MC,CN=BC,∠ACM=∠BCN=60°,
∴∠ACM+∠MCN=∠BCN+∠MCN,
即∠ACN=∠MCB,
在△ACN和△MCB中,
∵$\left\{\begin{array}{l}{AC=CM}\\{∠ACN=∠MCB}\\{CN=BC}\end{array}\right.$,
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)AN=BM,理由是:
如图2,∵四边形ACMF和四边形CBEN都是正方形,
∴AC=CM,BC=NC,∠ACN=∠BCM=90°,
在△ACN和△MCB中,
∵$\left\{\begin{array}{l}{AC=CM}\\{∠ACN=∠MCB}\\{NC=BC}\end{array}\right.$,
∴△ACN≌△MCB(SAS),
∴AN=BM.
点评 本题考查了全等三角形的性质和判定、正方形的性质,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.


科目:初中数学 来源: 题型:解答题
| 品名 | 黄瓜 | 茄子 |
| 批发价/(元/千克) | 2.4 | 2.2 |
| 零售价/(元/千克) | 3.6 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 100 | 150 | -400 | 350 | -100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) | 5-$\frac{x}{5}$ |
| 捕捞量(kg) | 950-10x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com