
分析 (1)将两点代入,运用待定系数法求解;
(2)把y=5代入y=2x+3解得,x=1,然后根据一次函数是增函数,进而得到关于x的不等式kx+b≥5的解集是x≥1.
解答 解:(1)∵一次函数y=kx+b的图象经过点(1,5)和(-1,1),
∴$\left\{\begin{array}{l}{k+b=5}\\{-k+b=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=3}\end{array}\right.$
∴函数解析式为:y=2x+3;
(2)∵k=2>0,
∴y随x的增大而增大,
把y=5代入y=2x+3解得,x=1,
∴当x≥1时,函数y≥5,
故不等式kx+b≥5的解集为x≥1.
点评 本题考查待定系数法求函数解析式,一次函数与一元一次不等式,关键是掌握数形结合思想.认真体会一次函数与一元一次不等式之间的内在联系.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:选择题
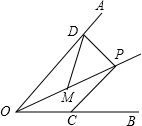 如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
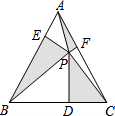 如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )
如图,等边△ABC中,P为三角形内一点,过P作PD⊥BC,PE⊥AB,PF⊥AC,连结AP、BP、CP,如果S△APF+S△BPE+S△PCD=$\frac{9\sqrt{3}}{2}$,那么△ABC的内切圆半径为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 听写正确的个数x | 组中值 |
| A | 0≤x<8 | 4 |
| B | 8≤x<16 | 12 |
| C | 16≤x<24 | 20 |
| D | 24≤x<32 | 28 |
| E | 32≤x<40 | 36 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com