
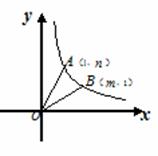
如图平面直角坐标系中,点A(1,n)和点B(m,1)为双曲线y= 第一象限上两点,连结OA、OB.
第一象限上两点,连结OA、OB.
(1)试比较m、n的大小;
(2)若∠AOB=30°,求双曲线的解析式.
科目:初中数学 来源: 题型:
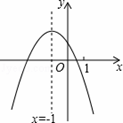
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②3b+2c<0;③m(am+b)<a﹣b;④ax2+bx+c<ax2+2ax-3a,其中正确结论的是 (填正确的序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
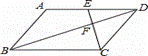
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△DEF:S△BCF =( )
A.4:9 B.1:4 C. 1:2 D.1:1
查看答案和解析>>
科目:初中数学 来源: 题型:
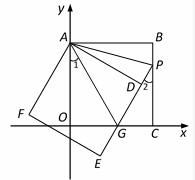
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式;
(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形,若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com