
��ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��3��3������������ABCO�Ƶ�A˳ʱ����ת�Ƕ�����0�㣼����90�㣩���õ�������ADEF��ED���߶�OC�ڵ�G��ED���ӳ��߽��߶�BC�ڵ�P����AP��AG��
��1����֤����AOG�ա�ADG��
��2�����PAG�Ķ��������ж��߶�OG��PG��BP֮���������ϵ��˵�����ɣ�
��3������1=��2ʱ����ֱ��PE�Ľ���ʽ��
��4���ڣ�3���������£�ֱ��PE���Ƿ���ڵ�M��ʹ��M��A��GΪ������������ǵ��������Σ������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵�����ɣ�
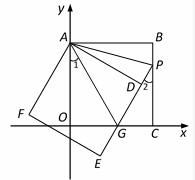
��1��֤����������ã�
AO=AD����AOG=��ADG=90�㣬
����Rt��AOG��Rt��ADG��AO=AD��AG=AG��
���AOG�ա�ADG��HL��. ����2��
��2����PAG =45��,PG=OG+BP.�������£�
�ɣ�1��ͬ����֤��ADP�ա�ABP�����DAP=��BAP��DP=BP��
���ɣ�1����AOG�ա�ADG�����1=��DAG��DG=OG��
�֡ߡ�1+��DAG+��DAP+��BAP=90�㣬
��2��DAG+2��DAP=90�㣬����DAG+��DAP=45�㣬���PAG=��DAG+��DAP=45��.
��PG=DG+DP=OG+BP. ����6��
��3���ߡ�AOG�ա�ADG�����AGO=��AGD��
�֡ߡ�1+��AGO=90�㣬��2+��PGC=90�㣬��1=��2�����AGO=��AGD=��PGC��
�֡ߡ�AGO+��AGD+��PGC=180�㣬���AGO=��AGD=��PGC=60�㣬���1=��2=30�㣬
��Rt��AOG��AO=3��OG=AOtan30��=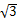 ��
��
��G������Ϊ��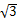 ��0����CG=3﹣
��0����CG=3﹣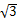 ��
��
��Rt��PCG��PC=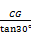 =
=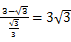 -3�� ��P����������3��
-3�� ��P����������3��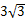 -3��
-3��
��ֱ��PE�Ľ���ʽΪy=kx+b��
��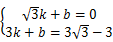 �� ���
�� ���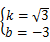
��ֱ��PE�Ľ���ʽΪy=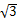 x﹣3. ����10��
x﹣3. ����10��
��4��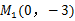 ��
��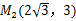 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�̵깺��600�����μ���Ʒ������Ϊÿ��6Ԫ����һ����ÿ��10Ԫ�ļ۸��۳�200�����ڶ�������ÿ��10Ԫ�ļ۸������Կ��۳�200�������̵�Ϊ���ʵ�����������������������,�����г����飬����ÿ����1Ԫ���ɶ��۳�50�������ۼ۲��õ��ڽ�
�ۣ����۽���xԪ��������һ�ܺ��̵��ʣ�����μ���Ʒ��ִ�������ÿ��4Ԫ�ļ۸�ȫ���۳�.
(1)�ǵڶ��ܼ����ܺ���̵��������ּ���Ʒ������ֱ�Ϊy1, y2,��ֱ����y1, y2����x�ĺ�������ʽ����4�֣�
(2)����������μ���Ʒ������1250Ԫ���ʵڶ���ÿ������Ʒ�����ۼ۸�Ϊ����Ԫ����4�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
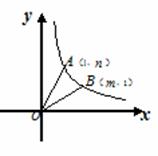
��ͼƽ��ֱ������ϵ�У���A��1��n���͵�B��m��1��Ϊ˫����y= ��һ���������㣬����OA��OB��
��һ���������㣬����OA��OB��
��1���ԱȽ�m��n�Ĵ�С��
��2������AOB=30�㣬��˫���ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м��㲻��ȷ����( )
A��������3���� =��1 B��
=��1 B�� +[������
+[������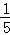 ��]=1 C����3+|��3|=0 D����
��]=1 C����3+|��3|=0 D����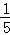 ��5=��
��5=��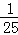
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ij��λһ����������������£�ӯ��Ϊ������+853.5Ԫ��+237.2Ԫ����325Ԫ��+138.5Ԫ����280Ԫ����520Ԫ��+103Ԫ����ô����һ�����ڸõ�λ��ӯ��ǿ���ӯ���������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������y = -x2��y������ƽ�����ɸ���λ���Ⱥ�����������x�����������Ͷ��㹹�ɵ���ֱ�������Σ����������ߵĽ���ʽΪ ��
= -x2��y������ƽ�����ɸ���λ���Ⱥ�����������x�����������Ͷ��㹹�ɵ���ֱ�������Σ����������ߵĽ���ʽΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com