
C
(1)观察图1,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(4分)
解:(1)连接AD并延长至点F,
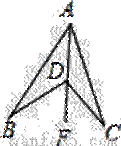 由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;
且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD;
∠BDC=∠BDF+∠CDF=∠BAD+∠B+∠C+∠CAD=∠B+∠C+∠BAC
所以∠BDC=∠B+∠C+∠BAC
(证明方法不唯一)
(2)请你直接利用以上结论,解决以下三个问题:
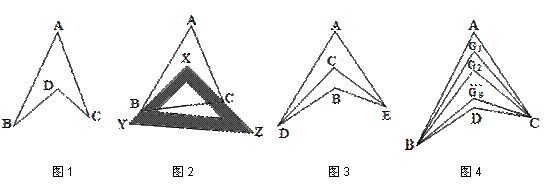
①∠ABX+∠ACX=___40°__.(3分)
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,
求∠DCE的度数;(4分)
(2)②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,
所以∠ADB+∠AEB=∠DBE -∠A=130°-50°= 80°;
因为 DC平分∠ADB,EC平分∠AEB21cnjy.com
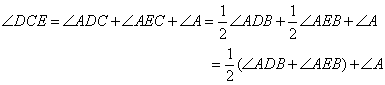 所以
所以
所以
因为∠ADB+∠AEB= 80°,∠A=50°,
所以 ∠DCE=90°;
③____70°__.


科目:初中数学 来源: 题型:
一次数学活动中,小杨同学利用自己制作的测角器测量小山的高度CD,如图11.已知她的眼睛与地面的距离为1.6米,小杨同学在B处测量时,测角器中的∠AOP=60°(测角器零度线AC和铅垂线OP的夹角);然后他向小山走50米到达点F处(点B、F、D在同一直线上),这时测角器中的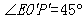 ,那么小山的高度CD约为多少米?(结果精确到小数点后一位)(参考数据:
,那么小山的高度CD约为多少米?(结果精确到小数点后一位)(参考数据: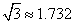 ,
,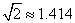 )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
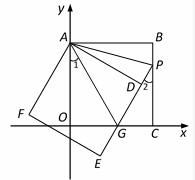
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式;
(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形,若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com